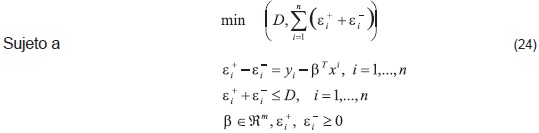MODELOS DE OPTIMIZACIÓN POR METAS PARA EL CÁLCULO DE ESTIMADORES EN REGRESIÓN MÚLTIPLE
GOAL OPTIMIZATION MODELS FOR THE ESTIMATORS CALCULUS IN MULTIPLE REGRESSION PROBLEMS
Héctor Andrés López Ospina1
Rafael David López Ospina2
1 Estudiante de Doctorado en Sistemas Complejos de Ingeniería. Universidad de Chile Msc. Matemática Aplicada. Matemático. Universidad Nacional de Colombia,
E-mail: hlopezospina@ing.uchile.cl
2 Estadístico. Universidad Nacional de Colombia. Estadístico Banco Agrario,
E-mail: rdlopezo@unal.edu.co
Fecha de recepción: 3 de enero de 2010 Fecha de aceptación: 24 de mayo de 2010
RESUMEN
Este trabajo introductorio presenta y describe diversos modelos de regresión múltiple y su respectiva formulación como un problema de optimización por metas. Se describen los modelos de regresión mediana, regresión mediana ponderada, regresión cuantílica, regresión cuantílica ponderada y formulación minimax. Además, se describe la formulación dual de estos modelos y se presentan algunos ejemplos sencillos se presentan para explicar los conceptos desarrollados y las aplicaciones de dichos modelos en ingeniería y ciencias.
Palabras clave: modelos de regresión múltiple, programación por metas, regresión cuantílica, optimización minimax, regresión restringida.
ABSTRACT
This introductory work shows several multiple regression models and their relevant development as a problem of goal programming (eliminar...optimization by goals). It describes the median regression, weighted median regression, quantile regression, weighted quantile regression, and minimax formulation models. Furthermore, describes their dual formulation. We describe some simple examples to explain the concepts developed and applications of such models on engineering and sciences.
Key words: multiple regression models, goal programming, quantile regression, minimax optimization, constrained regression.
INTRODUCCIÓN
Uno de los grandes problemas de los modelos de regresión lineal múltiple es el cumplimiento de los supuestos básicos como homocedasticidad, valor esperado y normalidad de los errores, etc. El presente documento tiene por objetivo relacionar algunos modelos poco usados en la aplicación econométrica y útiles para el análisis de la información. Además, se integra la modelación estadística con los modelos de optimización con múltiples objetivos.
Los modelos de regresión múltiple son algunas de las técnicas estadísticas más usadas para analizar datos. El objetivo de los modelos de regresión múltiple es encontrar la relación entre variables. De manera más formal, dados n vectores en 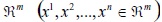 , que representan las variables explicativas y n valores reales
, que representan las variables explicativas y n valores reales 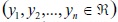 , que representan la variable explicada. en estos modelos, se tiene por objetivo encontrar un vector de estimadores
, que representan la variable explicada. en estos modelos, se tiene por objetivo encontrar un vector de estimadores 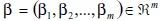 que minimicen un problema determinado de optimización que depende de los valores de xi, yi, i = 1,...,n. la regresión por mínimos cuadrados busca resolver este tipo de problemas de optimización [18]:
que minimicen un problema determinado de optimización que depende de los valores de xi, yi, i = 1,...,n. la regresión por mínimos cuadrados busca resolver este tipo de problemas de optimización [18]:
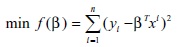
Y además, supone lo siguiente:
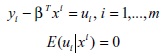
Siendo ui una sucesión de variables aleatorias e idénticamente distribuidas (generalmente, se asume la distribución normal).
En muchos problemas prácticos, los supuestos descritos anteriormente no se satisfacen con facilidad y es necesario, hacer algún tipo de transformaciones sobre las variables o utilizar otro tipo de técnicas matemáticas. Para dar solución a este tipo de problemas, surgen los conceptos de regresión mediana [28], y regresión cuantílica [2], [8], ya que se ha demostrado que estos tipos de modelos de regresión son más eficientes que el estimador máximo verosímil de muchos modelos paramétricos convencionales.
Existen diversas aplicaciones de dichas técnicas en áreas tales como: ecología [1 ] y [2], economía [3], [5], [6], retribución salarial [19], [29] y [12], predicción de demanda [16], calidad de la educación [4] y [38], desnutrición infantil [39], entre otros [7], [10], [11 ], [15], [17], [20], [21], [25] y [28]. En la sección siguiente, se presenta una breve introducción a la programación por metas. En la sección 2, se hace la formulación de diversos modelos de regresión, por medio de esta técnica de programación lineal multiobjetivo.
1. PROGRAMACIÓN POR METAS
La programación u optimización por metas (goal programming), [24], [27], [36] y [37] tiene por objetivo alcanzar unas metas o niveles de logro para determinados objetivos y fue desarrollada por Charnes y Cooper en 1955. De acuerdo con Güneş [33], la programación por metas (GP), es una técnica o herramienta muy útil para los tomadores de decisiones de tal forma que sea factible discutir y encontrar un conjunto de soluciones apropiadas y aceptables en problemas de decisión con múltiples objetivos o criterios. Por otra parte, determinar con precisión el valor real de cada objetivo es muy difícil por que se obtiene sólo información parcial.
Matemáticamente, los problemas de programación por metas se definen de la siguiente manera: dadas n funciones objetivo Z(x) = (Z1(x) Z2(x),...,Zn(x)), donde 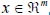 define el vector de variables de decisión y un vector de metas zmeta = (z1,meta,z2,meta,z3,meta,...,zn,meta) , donde zi,meta define la meta del objetivo i, el método ofrece como solución el punto factible más cercano a dicho punto. Así pues, el modelo matemático que representa dicha situación es:
define el vector de variables de decisión y un vector de metas zmeta = (z1,meta,z2,meta,z3,meta,...,zn,meta) , donde zi,meta define la meta del objetivo i, el método ofrece como solución el punto factible más cercano a dicho punto. Así pues, el modelo matemático que representa dicha situación es:
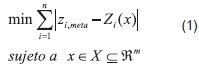
Donde X simboliza la región factible del problema de optimización.
La función objetivo del problema (1) es no lineal y no diferenciable. Sin embargo, es posible transformarla en una función lineal, introduciendo dos variables auxiliares positivas para cada objetivo, que son:
-
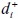 corresponde a la desviación positiva o variable de exceso en cuanto al cumplimiento de la meta i, i = 1,...,n.
corresponde a la desviación positiva o variable de exceso en cuanto al cumplimiento de la meta i, i = 1,...,n.
-
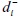 correspondiente a la desviación negativa o faltante sobre el nivel requerido para la meta i, i = 1,...,n.
correspondiente a la desviación negativa o faltante sobre el nivel requerido para la meta i, i = 1,...,n.
Además, se cumple que 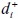
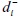 = 0 con i, i = 1,...,n. es decir, no es posible que una variable de desviación positiva y una variable de desviación negativa pertenezcan de forma simultánea a la solución básica, ya que en ningún caso se puede exceder y ser inferior a la meta. Por otra parte:
= 0 con i, i = 1,...,n. es decir, no es posible que una variable de desviación positiva y una variable de desviación negativa pertenezcan de forma simultánea a la solución básica, ya que en ningún caso se puede exceder y ser inferior a la meta. Por otra parte:
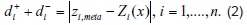
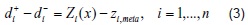
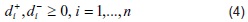
Utilizando (2), (3) y (4), el problema de optimización (1) se puede escribir de la siguiente manera:
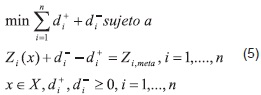
En algunos casos, los problemas de programación por metas pueden tener diferentes niveles de ponderación para cada objetivo. En este caso, la función objetivo se escribe de la siguiente forma:
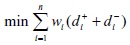
Donde wi es la ponderación de la meta i. existen algunas variantes de la formulación descrita anteriormente desarrolladas en Smith R., et al [24].
Otro tipo de formulaciones que se usan en programación por metas, es la basada en la minimización de la distancia o norma Lp del valor obtenido a la meta. La formulación general del problema de optimización es [41], [42], y [43]:
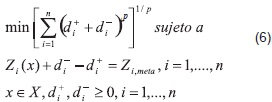
Donde p ∈ [1,+∞]. La formulación anterior implica tener una función objetivo no diferenciable; para evitarla se resuelve el siguiente problema equivalente de optimización:
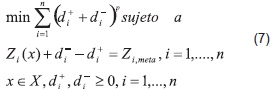
Cuando p=1, se tiene el problema lineal de programación por metas descrito en (5). Cuando se tiene la norma del máximo (p = ∞), la formulación de la función objetivo se presenta de la siguiente forma minimax [44]:
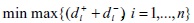
El modelo (7) para la norma del máximo, tiene la siguiente formulación basada en la norma de Chevyshev [44], [45]:
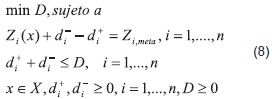
Donde D es una cota superior de las suma de las desviaciones con respecto de la meta en cada uno de los n objetivos. La formulación minimax es típica de los problemas aplicados en teoría de juegos o teoría de la decisión multicriterio [46], [47] y [48].
Vale la pena anotar que existen muchas aplicaciones de la programación por metas, en las cuales se utiliza la formulación original combinada con otras estrategias de modelación como programación lineal difusa aplicada a diversos sectores y temas específicos [30], [37]. Análisis envolvente de datos [31], modelación en cadenas de abastecimiento, Planeación de la producción y localización de entes físicos [32], [49], [50], Planeación de recursos humanos [34] y Gestión financiera [35], [37].
2. REGRESIÓN MEDIANA
La regresión mediana o L1 descrita en Toshiyuki S. et al [26] y Li, Y. et al [40] tiene por objetivo minimizar la suma de errores absolutos. es decir:
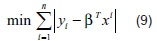 Haciendo εi = yi - βTxi, donde εi representa el error o desviación del valor estimado sobre el valor real. Si εi > 0, la estimación βTxi < yi (el valor real (yi), es menor que el valor estimado βTxi). en caso contrario, el valor real observado es menor que el valor estimado. defínase:
Haciendo εi = yi - βTxi, donde εi representa el error o desviación del valor estimado sobre el valor real. Si εi > 0, la estimación βTxi < yi (el valor real (yi), es menor que el valor estimado βTxi). en caso contrario, el valor real observado es menor que el valor estimado. defínase:
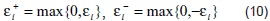
Que representan variables de desviación o errores en las estimaciones. Por lo desarrollado en la sección 1, el modelo de optimización (9) formulado por medio de programación por metas es [26]:
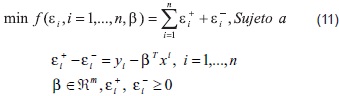
El problema de programación lineal (11) tiene m + 2n variables y n restricciones. Las restricciones del modelo de optimización (11) representan la desviación (positiva o negativa), de la estimación con respecto del valor real y la función objetivo es equivalente a la minimización de los errores absolutos.
Ejemplo 1. Tomado de Montgomery, et al [18]. La tabla 1 presenta algunos datos de pruebas de energía solar térmica, donde:
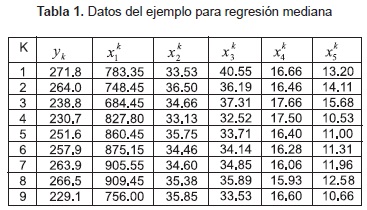 y: flujo total del calor (Kwatts)
y: flujo total del calor (Kwatts)
x1: insolación (watts/m2)
x2: posición del foco en dirección este (pulgadas)
x3: posición del foco en dirección sur (pulgadas)
x4: posición del foco en dirección norte (pulgadas)
x: hora del día
Por mínimos cuadrados el modelo de optimización es:
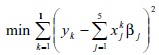
Obteniendo la solución de la tabla 2:

Por otro lado, utilizando regresión mediana se obtiene el siguiente modelo:
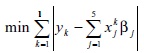
Y su formulación por medio de programación por metas:
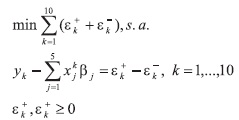
El conjunto de restricciones del problema anterior, define el error (desviación positiva o negativa), del valor real yk con respecto de la estimación 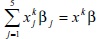 . Por ejemplo: para la primera observación (k = 1), la restricción obtenida es:
. Por ejemplo: para la primera observación (k = 1), la restricción obtenida es:
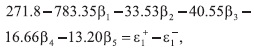
De este modelo de regresión L1 los estimadores obtenidos son López H. [13].

Además, se puede hacer las siguientes comparaciones para los dos modelos:
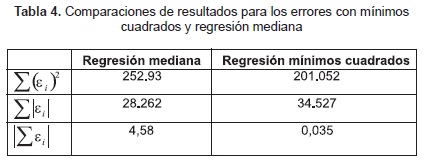
Aunque los resultados obtenidos por mínimos cuadrados parecen mejores que los resultados obtenidos con regresión mediana, es importante anotar que sus objetivos son distintos ya que no es necesario hacer los mismos supuestos sobre los errores.
Ejemplo 2. Polinomio de regresión. Supongamos que se tienen los datos de la tabla 5 de la demanda anual de un producto para ser ajustados por una función polinomial de orden 2.

La ecuación del polinomio de regresión está dada por: d = β0 +β1x + β2x2. Luego el modelo por programación por metas es:
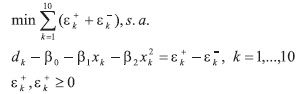
Por ejemplo: para k = 5, la restricción sería:
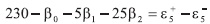
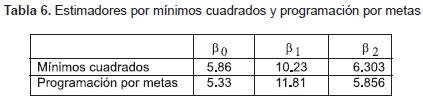
Obteniendo la solución por medio de mínimos cuadrados y por programación por metas que se presenta en la tabla 6:
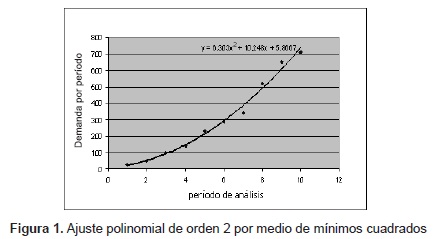
Gráficamente el polinomio solución se representa en la siguiente figura 1:
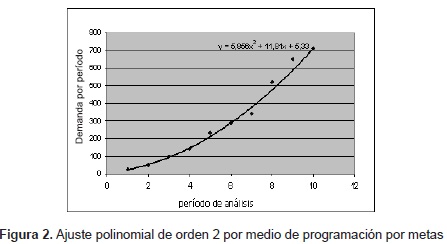
Ejemplo 3. Infuencia de datos atípicos. Una de las grandes desventajas de la regresión por mínimos cuadrados, es la influencia de datos atípicos. Por ejemplo: los datos descritos en la tabla 7, representan la demanda de un artículo en determinados períodos.
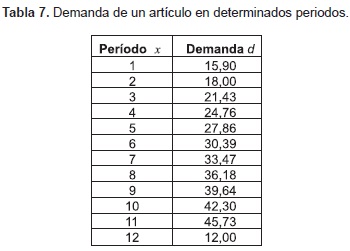
En la figura 3, se presenta un diagrama de dispersión de la información anteriormente descrita.
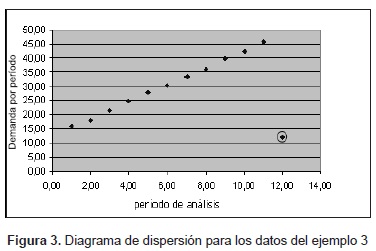
Se podría asociar dicho comportamiento con una recta de regresión, notando que el último dato no sigue la tendencia esperada. Utilizando mínimos cuadrados, la ecuación obtenida es:
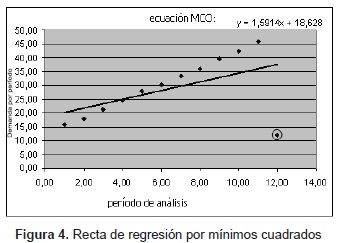
Utilizando regresión mediana, se obtienen la siguiente ecuación y recta de regresión:
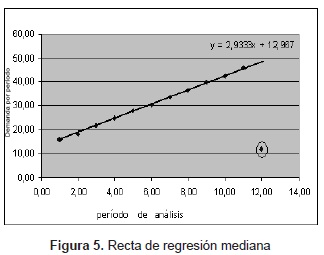
Es posible darse cuenta de que en regresión mediana o con percentil 50, la influencia de datos atípicos es menor que en los modelos por mínimos cuadrados [8], debido a que dicha medida de tendencia es más robusta que el promedio.
Según lo indica [56], existen antecedentes teóricos, tales como lo demostrado en [57], donde se afirma que en los casos en los cuales existen datos atípicos o anómalos la regresión mediana es más consistente que por mínimos cuadrados. De esta forma, utilizando dicha técnica es posible no eliminar estos datos de la muestra. Por otra parte, Dielman T. [58], demuestra que en el caso de no tener residuos normales en mínimos cuadrados, esta situación no genera problemas en la formulación presentada en este trabajo, debido a que es posible extenderlo a otro tipo de distribuciones.
3. REGRESIÓN CUANTÍLICA O POR PERCENTILES
En los métodos de regresión lineal clásicos, el objetivo es minimizar la suma de los residuales al cuadrado y utilizar la media como estimador. Por otra parte, la regresión cuantílica o por percentiles introducida por Koenker [8], y Koenker et al [9], donde se busca minimizar una suma de errores con pesos asimétricos y utilizar los cuantíles como estimadores. La motivación para utilizar cuantíles en vez de la media, es debido a la relación estocástica que puede existir en las variables aleatorias trabajadas en los modelos, siendo posible reflejar una mejor relación y encontrar menor impresión en las inferencias realizadas. La estimación por mínimos cuadrados puede llegar a ser muy deficiente cuando los errores no distribuyen normal. En el caso de la regresión cuantílica, las estimaciones generan modelos más robustos y por consiguiente más confiables. El problema de la regresión por mínimos, que busca estimar funciones mediante el promedio, es la poca robustez de dicha medida y además, dada la heterogeneidad de la variable explicada en algunos casos, es posible que el promedio sea una medida muy pobre para realizar el análisis de la información.
Los modelos de regresión cuantílica generalizan el modelo de regresión mediana (11). En este caso, no es necesario que 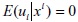 , pero el τ - ésimo cuantil o percentil del error con respecto de las variables regresoras debe ser cero.
, pero el τ - ésimo cuantil o percentil del error con respecto de las variables regresoras debe ser cero.
Cabe anotar que las condiciones para aplicar los modelos de regresión cuantílica son menos fuertes que los modelos por mínimos cuadrados. En este caso, se realiza la estimación del τ - ésimo cuantil o percentil de las variables explicadas yi con respecto de las variables regresoras, que se anota de la siguiente forma:
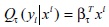
La estimación de βt se encuentra por medio de:
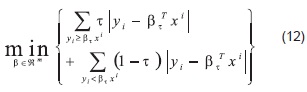
Es decir, los errores positivos se ponderan con un valor de τ y los errores negativos se ponderan con un valor de (τ -1). Una manera más compacta de escribir el problema de optimización (12) es por medio de la función de chequeo definida de la siguiente manera:
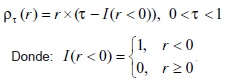
De este modo, el modelo matemático (12) se puede escribir como:
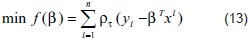
Cuando τ = 0.5, el problema de regresión cuantílica es equivalente al problema de regresión mediana.
La técnica más usada para solucionar el problema de regresión cuantílica (13), es por medio de su representación como un problema de programación lineal por metas [14]. La función de chequeo se puede escribir como la suma de dos funciones positivas:
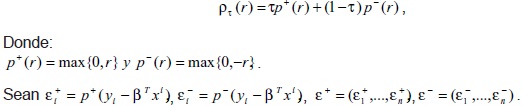
De esta forma, la formulación del problema de regresión cuantílica (13), como un problema de programación lineal por metas, está dada por Koenker, R., [8]:
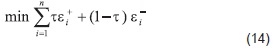
Sujeto a
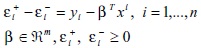
En este caso, las restricciones son equivalentes a las del problema de regresión mediana.
La función objetivo cambia por las ponderaciones asimétricas de las variables de desviación. A continuación, se muestra un caso de aplicación de la regresión cuantílica con una sola variable explicativa.
Ejemplo 4. Los datos presentados a continuación son simulados. Sea x = años invertidos en educación y la variable explicada y = retribución salarial por hora en unidades monetarias. El diagrama de dispersión para los datos es el siguiente:
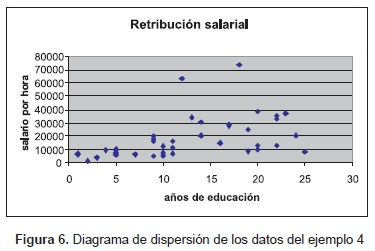
Obteniendo las curvas de regresión por percentiles con el paquete estadístico R [22], descritas en la figura 7, con los valores de τ =0.10, 0.25, 0.5, 0.75 y 0.9.
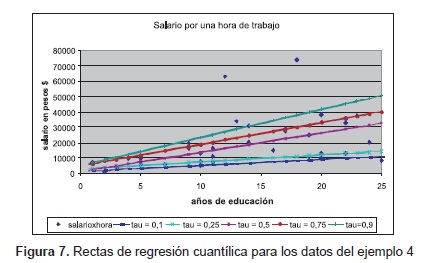
Análisis de resultados. Por ejemplo: la curva obtenida para τ = 0.1 es y = 1.3 +384x, implica que para los elementos de la población con menor salario (inferior al 10% o por debajo del percentil 10), se tendrá que por cada año adicional invertido en educación, su aumento promedio salarial por hora es de 384 unidades monetarias. Otra aplicación importante en este ejemplo, es la siguiente: para una persona que ha estudiando 16 años, se obtienen las siguientes estimaciones en los percentiles 10 y 90:
y10(16) = 7472 unidades monetarias
y90(16) = 34306 unidades monetarias
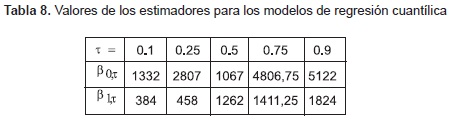
Como en ese rango se encuentra el 80% de la población, se espera que con dicho nivel de estudio (16 años), la retribución salarial por hora de los individuos se encuentre entre esas dos estimaciones. En la tabla 8, se presenta el valor β0,τ y β1,τ para los distintos modelos de regresión cuantílica de la gráfica 7, recordando que la recta de regresión para el percentil τ se nota: yτ = β0,τ y β1,τ x .
4. REGRESIÓN CUANTÍLICA PONDERADA
En regresión, uno de los objetivos de los modelos por mínimos cuadrados ponderados es corregir problemas tales como varianza no constante para los errores o simplemente dar una jerarquía o nivel de importancia a cada una de las observaciones. En este tipo de modelos, es necesario introducir un nuevo parámetro definido de la siguiente forma:
w = (w1,w2 ,...,wn )
Cada wi representa el factor de ponderación de la observación i, i = 1,...,n.
El problema de optimización para mínimos cuadrados ponderados se formula de la siguiente manera Montgomery, et al [18]:
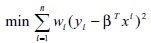
Por otra parte, el modelo de regresión cuantílica ponderada se escribe como:
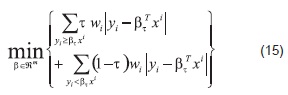
De forma equivalente (15), se expresa como un modelo de programación por metas de la siguiente manera:
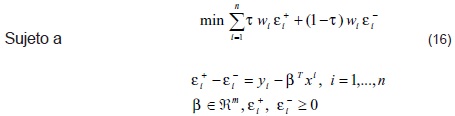
En el caso que wi =1, i = 1,...,n el problema (16) es equivalente a (14). Cuando wi =1, i =1,...n y 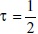 el problema (16) es equivalente al problema de regresión mediana (11). Matricialmente (16), se expresa de la siguiente manera:
el problema (16) es equivalente al problema de regresión mediana (11). Matricialmente (16), se expresa de la siguiente manera:
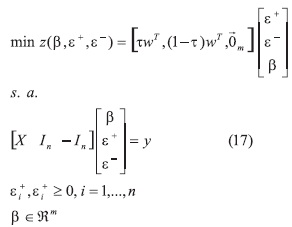
Nótese que una ventaja de esta formulación por metas, es que permite incluir restricciones sobre los parámetros [56], por conocimientos a priori, tales como intervalos de pertenencia (cotas superiores e inferiores), relaciones entre parámetros, signos, etc., extendiendo la formulación clásica de mínimos cuadrados ordinarios. Estas restricciones sobre los parámetros controlan valores no factibles de los estimadores y problemas de mal ajuste [59]. A continuación, se presenta un ejemplo para mostrar una de las utilidades de la regresión cuantílica ponderada.
Ejemplo 5. Con los datos del ejemplo 4, se obtiene la curva de regresión cuantílica con τ = 0.9 y dada por: y90 = 5122 + 1824x. Una de las aplicaciones de los modelos de regresión ponderados es en la influencia de datos atípicos. En este caso, se encuentran dos datos fuera del comportamiento promedio de la población.
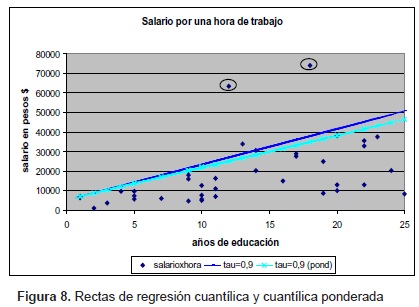
Para evitar la influencia de dichos datos, se hace una ponderación dándole menor importancia. Se observa que en el modelo de regresión cuantílica con τ = 0.9 ponderado, la estimación promedio es menor. Es importante anotar que los datos atípicos sólo influyen en los percentiles extremos. Otra aplicación de los modelos ponderados de mayor uso, es cuando se tienen factores de expansión por muestreo [23].
5. MODELO DUAL DE OPTIMIZACIÓN
Es posible asociar a (17), un problema de programación lineal dual [3]. Sea d = [d1,...,dn]T, el vector de variables duales correspondiente al problema (14). Así, el dual asociado al problema anterior es:
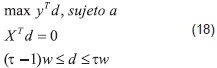
El problema dual es un problema de programación lineal con variables acotadas y tiene m+2n restricciones y n variables. Es decir, son menos variables que en problema primal (17). En la práctica, es más fácil resolver el problema dual para regresión cuantílica ponderada que el primal. Algebraicamente, el modelo matricial (18) se escribe de la siguiente manera:
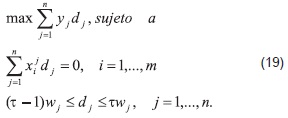
6. FORMULACIÓN DEL PROBLEMA DE OPTIMIZACIÓN POR METAS CUADRÁTICO Y MINI-MAX
La norma Lp aplicada a los modelos de regresión lineal múltiple tiene por objetivo minimizar la siguiente función objetivo:
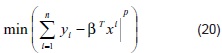
Haciendo εi = yi - βTxi, donde εi representa el error o desviación del valor estimado sobre el valor real. Si se define 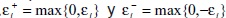 son las variables de desviación o errores en las estimaciones. De acuerdo con lo desarrollado en la sección 1, el modelo de optimización (20) formulado por medio de la programación por metas no lineal es:
son las variables de desviación o errores en las estimaciones. De acuerdo con lo desarrollado en la sección 1, el modelo de optimización (20) formulado por medio de la programación por metas no lineal es:
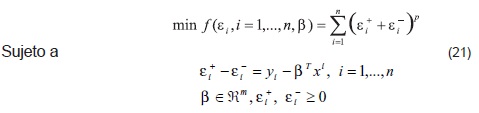
Claramente cuando p=2, se tiene el problema típico de regresión por mínimos cuadrados, y se obtiene una formulación de optimización por metas equivalente a la formulación clásica de econometría [51], [52] y cuando p=1, se tiene el problema de regresión mediana. Un caso interesante es cuando p=∞, debido a que se tiene el siguiente problema de regresión múltiple min y max:
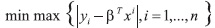
Que de forma equivalente, se puede escribir como un problema de programación por metas de la siguiente forma:
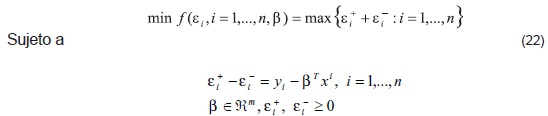
Como el problema anterior no es diferenciable en su función objetivo, entonces al añadir una cota superior a todas las sumas de las desviaciones [27], el problema anterior es equivalente a: min D
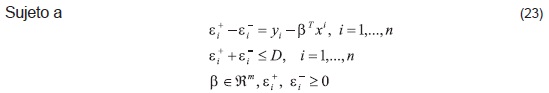
Nótese que en este caso, se minimiza la máxima desviación de los residuos (D), y se encuentra un modelo más equilibrado que los modelos clásicos [60]. Debido a que esta formulación se basa en el máximo de una muestra, esta medida no es robusta ante la presencia de datos atípicos, por lo cual se sugiere su uso en el caso de una muestra homogénea [56].
Aznar y et al [56], proponen cambiar el conjunto de restricciones 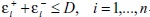 por restricciones de la forma
por restricciones de la forma 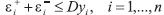 cuando se están estimando precios, viajes o cualquier variable positiva.
cuando se están estimando precios, viajes o cualquier variable positiva.
La formulación minimax para modelos de regresión múltiple tiene aplicaciones en varias ramas de la estadística e ingeniería, tal como regresión robusta [53] y [54], regresión local [55], estadística no paramétrica, etc.
Algunos autores proponen el uso de un modelo biobjetivo [56], de tal forma que se pueda incluir la máxima desviación de los errores y la regresión mediana (siendo esta una técnica excelente en el caso de datos atípicos en la muestra), y llegar a soluciones intermedias por medio de la generación de la frontera de Pareto. Matemáticamente, el problema biobjetivo se escribe como:
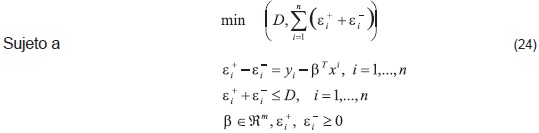
Esta formulación es interesante, debido a que es posible utilizar técnicas clásicas de optimización multiobjetivo [24] para analizar el conjunto de soluciones y su implicación en la estimación y predicción.
7. CONCLUSIONES
Los modelos de programación multiobjetivo por metas, son una herramienta útil para el cálculo de estimadores en modelos de regresión múltiple debido a su formulación equivalente.
Es interesante aplicar estos modelos de regresión cuantílica y mediana cuando los supuestos sobre los errores en mínimos cuadrados no se cumplen de forma satisfactoria o de forma completa. Además, las formulaciones como un problema de programación por metas, permite incluir restricciones sobre los parámetros por estimar y de esta forma, controlar a priori condiciones no factibles o conocimiento dado sobre los estimadores.
Los modelos de regresión mediana permiten menor influencia de datos atípicos con respecto de los modelos de regresión por mínimos cuadrados. De esta forma, utilizando dicha técnica, es posible no eliminar estos datos de la muestra.
La regresión cuantílica permite analizar la distribución de la variable respuesta en distintos puntos y determinar rangos en la predicción para un individiduo determinado.
La estimación por mínimos cuadrados puede llegar a ser muy deficiente cuando los errores no distribuyen normal. En el caso de la regresión cuantílica, las estimaciones generan modelos más robustos y por consiguiente, más confiables. El problema de la regresión por mínimos cuadrados, que busca estimar funciones con el promedio, es la poca robustez de dicha medida y además, dada la heterogeneidad de la variable explicada en algunos casos, es posible que el promedio sea una medida muy pobre para realizar el análisis de la información.
La programación por metas permite formular modelos de optimización que involucren el valor absoluto en la función objetivo (optimización no diferenciable), como un problema de programación lineal, introduciendo variables de desviación.
AGRADECIMIENTOS
Los autores agradecen los valiosos comentarios, sugerencias y observaciones de los evaluadores anónimos.
REFERENCIAS BIBLIOGRÁFICAS
[1] Cade B., Noon B., (2003) "A Gentle Introduction to Quantile Regression for Ecologists", Frontiers in Ecology and the Environment 1(8), 412-420.
[2] Cade B., Terrell J., y Schroeder R.; (1999) Estimating effects of limiting factors with regression quantiles, Ecology, 80, 311-323.
[3] Chernozhukov, V. and L. Umantsev. 2001. "Conditional Value-at-Risk: Aspects of Modeling and Estimation." Empirical Economics. March, 26:1, pp. 271-92.
[4] Eide E., y Showalter M., (1998) The effect of school quality on student performance: a quantile regression approach, Economics Letters, 58, 345-50.
[5] Engle Robert and Simone Manganelli.; (1999) "CaViaR: Conditional Autoregressive Value at Risk by Regression Quantiles." University of California, San Diego, Department of Economics Working Paper.
[6] Fitzenberger B., Koenker R., Machado J., A.F. (Eds.); (2002) Economic Applications of Quantile Regression. Series: Studies in Empirical Economics. Vl, 324 p. 74 illus., Hardcover.
[7] Knight K., Bassett G., y Mo-Yin S. Tam.; (2002) "Comparing Quantile Estimators for the Linear Model." Preprint.
[8] Koenker R., (2005) Quantile Regression, Econometric Society Monographs, Cambridge University Press.
[9] Koenker R., Basset G.; (1978) Regression Quantiles. Econometrica 46, 33-50.
[10] Koenker R., Geiling O.; (2001) 'Reappraising medfy longetivity: A quantile regression approach', Journal of American Statistic Association 96, 458-468.
[11] Koenker R., Machado J.; (1999) 'Goodness of ft and related inference processes for quantile regression', Journal of the American Statistical Association 94, 1296- 1310.
[12] López R., (2007) La brecha de la distribución salarial en Colombia, un efecto de discriminación?. Monografía de pregrado. Carrera de estadística. Universidad Nacional de Colombia.
[13] López H.; (2006) Introducción a GAMS y su aplicación en la solución de modelos matemáticos de optimización, in 'Memorias del XXII Coloquio distrital de Matemáticas y Estadística', Universidad Nacional de Colombia, Bogotá.
[14] López H., Mora H.; (2007) Cálculo de los estimadores de regresión cuantílica lineal por medio del método ACCPM. Revista Colombiana de Estadística 30 (1). 53 a 68.
[15] Ma L., Koenker R.; (2003) Quantile regression methods for recursive structural models, Technical report.
[16] Manning W., Blumberg L., y Moulton L.; (1995) The demand for alcohol: the differential response to price, Journal of Health Economics, 14, 123-148.
[17] McKeague I., Subramanian S., y Sun Y. Q.; (2002) Median regression and the missing information principle, Journal of Nonparametric Statistics 13, 709-727.
[18] Montgomery Peck, y Vining; (2004) Al análisis de regresión lineal. 3ª edición. editorial CECSA.
[19] Poterba James, and Kim Rueben; (1995) "The Distribution of Public Sector Wage Premia: New Evidence Using Quantile Regression Methods." NBER Working Paper No. 4734.
[20] Powell J.l.; (1986) 'Censored regression quantiles', Journal of Econometrics 32, 143-55.
[21] Powell J.; (2002) Notes On Median and Quantile Regression. Department of Economics. University of California, Berkeley.
[22] R. Development Core Team (2006), R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. *http://www.R-project.org.
[23] Särndal C. Swensson B., Wretman J., Model Assisted Survey Sampling. Springer Series in Statistics. Segunda Edición. 2003.
[24] Smith R., Mesa O., Dyner I., Jaramillo P., Poveda G., Valencia D.; (2000) Decisiones con múltiples objetivos e incertidumbre. 2a Edición. Facultad de Minas. Universidad Nacional de Colombia. Sede Medellín.
[25] Sosa Escudero W.; (2006) Perspectivas y Avances Recientes en Regresion por Cuantiles, en Marchionni, M. (editora), Ahumada, H., Jorrat, J., Navarro, M. y Sosa Escudero, W., Progresos en Econometría, Temas Grupo Editorial, Buenos Aires.
[26] Toshiyuki S., Yih-long C.; (1989) Goal Programming Approach for Regression Median. Decision Sciences 20 (4), 700-713.
[27] Winston W., Investigación de operaciones: aplicaciones y algoritmos. Séptima edición. Editorial Thomson. 2005.
[28] Wooldridge, J.M.; (2002) Econometric Analysis of Cross Section and Panel Data, The MIT Press, Cambridge, Massachusetts.
[29] Zarate, H.; (2002) Cambios en la estructura salarial: una historia desde la regresión cuantílica. CEMLA. Colombia.
[30] Dutta D., y Murthy S.; (2010) MULTI-CHOICE GOAL PROGRAMMING APPROACH FOR A FUZZY TRANSPORTATION PROBLEM. International Journal of Research and Reviews in Applied Sciences. Volume 2.
[31] Makui A., Alinezhad A., Kiani Mavi R., Zohrehbandian M.; (2008) A Goal Programming Method for Finding Common Weights in DEA with an Improved Discriminating Power for Efficiency. Journal of Industrial and Systems Engineering. Vol. 1, no. 4, pp 293-303.
[32] Mezghani M., Rebai A., Dammak A., Loukil T.; (2009) A goal Programming model for Aggregate Production Planning problem. International Journal of Operational Research. Vol. 4, No.1 pp. 23-3.
[33] Günes y Umarosman.; (2005) FUZZY GOAL PROGRAMMING APPROACH ON COMPUTATION OF THE FUZZY ARITHMETIC MEAN. Mathematical and Computational Applications, vol. 10, no. 2, pp. 211-220.
[34] Glynn J., College C.; (2005) A Goal Programming Approach To Human Resource Planning With A Concentration On Promotion Policy. Journal of Business & Economics Research . Volume 3, no. 3.
[35] Lin T., y O'Leary D., (1993) Goal programming applications in financial management. Advances in mathematical programming and financial planning, Volume 3, pages 211-229.
[36] Tamiz M., Jones D., y El-Darzi E., (1995) A review of Goal Programming and its applications. Annals of Operations Research. Volume 58, number 1.
[37] Dylan, Tamiz, Mehrdad, Ries, Jana (Eds.); (2010) New Developments in Multiple Objective and Goal Programming. Series: Lecture Notes in Economics and Mathematical Systems, Vol. 638.
[38] Marcenaro O., Navarro L., (2007) El éxito en la Universidad: Una aproximación cuantílica. Revista de Economía Aplicada Número 44 (vol. XV), págs. 5 a 39.
[39] Block S., Masters W., y Bhagowalia P.; (2010) Child Undernutrition, Household Poverty and National Income in Developing Countries: Quantile Regression Results. Selected Paper prepared for presentation at the Agricultural & Applied Economics Association.
[40] Li Y., y Zhu, J.; (2008) L1-norm quantile regressions, Journal of Computational and Graphical Statistics 17: 163-185.
[41] González-Pachón y Romero. (2001) Aggregation of partial ordinal rankings: an interval goal programming approach. Computers & Operations Research, Volume 28, issue 8. Pág. 827-834.
[42] Charnes A., Collomb B.; (1972) Optimal economic stabilization policy: Linear goal-programming models. Socieconomic Planning Sciences, Vol. 6. 431-5.
[43] Ignizio J.P.; (1974) Interval goal programming and applications. Documento de trabajo. Pennsylvania State University, USA.
[44] Du D., y Pardalos P.M.; (1995) Minimax And Applications, Kluwer, Wiley: Dordrecht.
[45] Demyanov V.F., y Molozemov N.V.; (1974) Introduction to Minimax. Wiley: New York.
[46] Rao S.S.; (1987) Game Theory approach for multiobjetive structural optimization. Computers & Structures. Volume 25. issue 1. Pag. 119-127.
[47] Aumann R., y Hart S.; (1994) Handbook of game theory with theory applications. Libro. Elsevier, 814 páginas.
[48] Simon D. A.; (2006) Game Theory Approach to constrained Minimax State Estimation. IEEE Transactions on signal Processing.
[49] Schniederjans M., Kwak N.K., y Helmer M.; (1982) An Application of Goal Programming to Resolve a site Location Problem. Interfaces. Vol 12. no. 3.
[50] Badri M.; (1999) Combining the analiytic hierchachy process and goal programming for global facility location-allocation problem. International Journal of Production Economics. Volume 62, issue 3, pág: 237-248.
[51] Greene W.H.; (1998) Análisis econométrico. Prentice Hall.
[52] Novales A.; (1996) Econometría. McGraw Hill.
[53] Wiens D.; (1990) Robust minimax designs for multiple linear regression. Linear Algebra and its Applications. Volume 127. Páginas 327-340.
[54] Huber P., y Ronchetti E.; (2009) Robust Statics. John Wiley and Sons. 354 páginas.
[55] Fan J.; (1993) Local Linear regression Smoothers and their minimax efficiencies. The Annals of Statistics. Vol, 21, no 1, 196-216.
[56] Aznar J., y Guijarro F.; (2004) Métodos de valoración basados en la programación por metas: modelo de valoración restringida. Estudios Agrosociales y Pesqueros. Numero 204. Pp 29-45.
[57] Basset G., y Koenker R.; (1978) Asymptotic theory of least absolute Errors. The American Statistician, 51 (2): pp. 99-105.
[58] Dielman T. A.; (1986) Comparison of forecasts from least absolute value and least squares regression. Journal of Forecasting, 5 (3): pp. 189-195.
[59] Charnes A., Cooper W. W., y Sueyoshi T.; (1986) Least squares/ridge regression and goal programming/constrained regression alternatives. European Journal of Operational Research, 27 (2). Pp. 146-157.
[60] Romero C.; (2001) Extended lexicographic goal programming: a unifying approach. Omega, 29 (1): pp. 63-71.
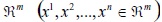 , que representan las variables explicativas y n valores reales
, que representan las variables explicativas y n valores reales 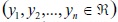 , que representan la variable explicada. en estos modelos, se tiene por objetivo encontrar un vector de estimadores
, que representan la variable explicada. en estos modelos, se tiene por objetivo encontrar un vector de estimadores 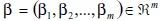 que minimicen un problema determinado de optimización que depende de los valores de xi, yi, i = 1,...,n. la regresión por mínimos cuadrados busca resolver este tipo de problemas de optimización [18]:
que minimicen un problema determinado de optimización que depende de los valores de xi, yi, i = 1,...,n. la regresión por mínimos cuadrados busca resolver este tipo de problemas de optimización [18]: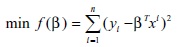
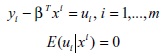
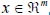 define el vector de variables de decisión y un vector de metas zmeta = (z1,meta,z2,meta,z3,meta,...,zn,meta) , donde zi,meta define la meta del objetivo i, el método ofrece como solución el punto factible más cercano a dicho punto. Así pues, el modelo matemático que representa dicha situación es:
define el vector de variables de decisión y un vector de metas zmeta = (z1,meta,z2,meta,z3,meta,...,zn,meta) , donde zi,meta define la meta del objetivo i, el método ofrece como solución el punto factible más cercano a dicho punto. Así pues, el modelo matemático que representa dicha situación es: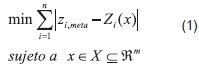
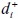 corresponde a la desviación positiva o variable de exceso en cuanto al cumplimiento de la meta i, i = 1,...,n.
corresponde a la desviación positiva o variable de exceso en cuanto al cumplimiento de la meta i, i = 1,...,n.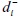 correspondiente a la desviación negativa o faltante sobre el nivel requerido para la meta i, i = 1,...,n.
correspondiente a la desviación negativa o faltante sobre el nivel requerido para la meta i, i = 1,...,n.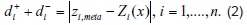
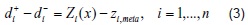
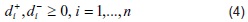
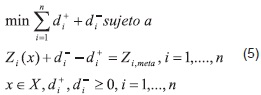
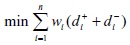
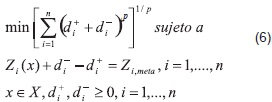
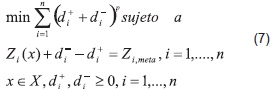
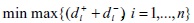
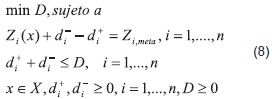
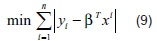
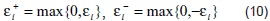
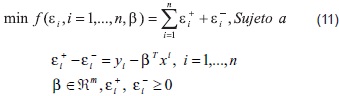

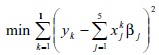

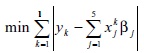
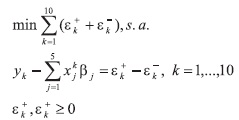
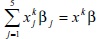 . Por ejemplo: para la primera observación (k = 1), la restricción obtenida es:
. Por ejemplo: para la primera observación (k = 1), la restricción obtenida es: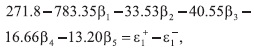



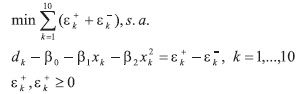
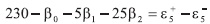







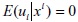 , pero el τ - ésimo cuantil o percentil del error con respecto de las variables regresoras debe ser cero.
, pero el τ - ésimo cuantil o percentil del error con respecto de las variables regresoras debe ser cero.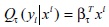
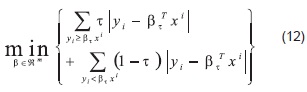
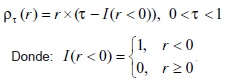
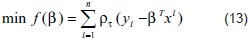
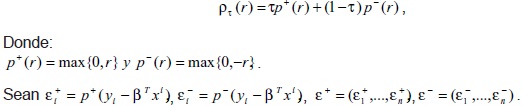
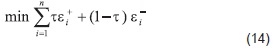
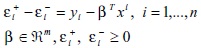



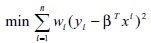
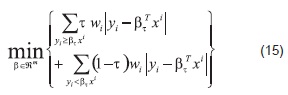
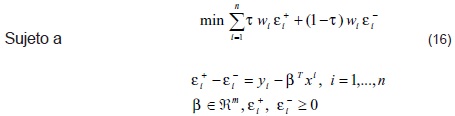
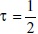 el problema (16) es equivalente al problema de regresión mediana (11). Matricialmente (16), se expresa de la siguiente manera:
el problema (16) es equivalente al problema de regresión mediana (11). Matricialmente (16), se expresa de la siguiente manera: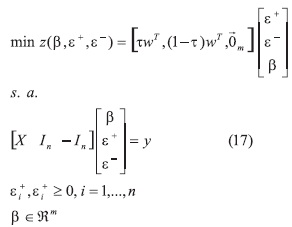

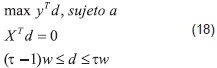
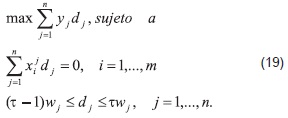
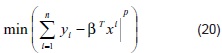
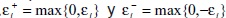 son las variables de desviación o errores en las estimaciones. De acuerdo con lo desarrollado en la sección 1, el modelo de optimización (20) formulado por medio de la programación por metas no lineal es:
son las variables de desviación o errores en las estimaciones. De acuerdo con lo desarrollado en la sección 1, el modelo de optimización (20) formulado por medio de la programación por metas no lineal es: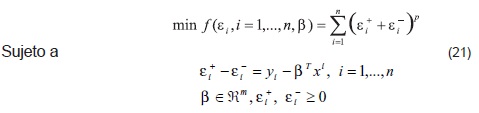
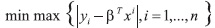
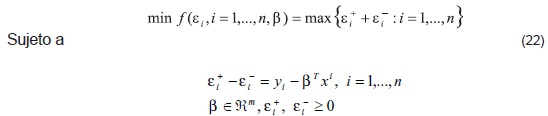
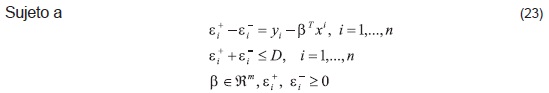
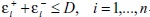 por restricciones de la forma
por restricciones de la forma 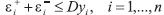 cuando se están estimando precios, viajes o cualquier variable positiva.
cuando se están estimando precios, viajes o cualquier variable positiva.