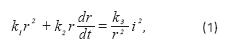
REGRESIÓN BAYESIANA LINEAL PARA CALIBRAR LOS PARÁMETROS DE UN MODELO DE HORNO DE ARCO
ESTIMATING ARC FURNACE MODEL PARAMETERSUSING BAYESIAN LINEAR REGRESSION
Jesser James Marulanda Durango
Ing. Electricista, MSc., Profesor Auxiliar, Facultad de Ingeniería,
Investigador Grupo de Electrónica de Potencia.
Universidad Tecnológica de Pereira, Pereira, Colombia.
jjmarulanda@utp.edu.co
Mauricio Alexander Álvarez López
Ing. Electrónico, PhD., Profesor Asociado, Facultad de Ingeniería,
Investigador Grupo de Automática.
Universidad Tecnológica de Pereira, Pereira, Colombia.
malvarez@utp.edu.co
Alfonso Alzate Gómez
Ing. Electricista, MSc., Profesor Titular, Facultad de Ingeniería,
Investigador Grupo de Electrónica de Potencia.
Universidad Tecnológica de Pereira, Pereira, Colombia.
alalzate@utp.edu.co
Fecha de recepción: 27 de abril de 2013 Fecha de aprobación: 16 de diciembre de 2013
RESUMEN
Este documento presenta la calibración de los parámetros de un modelo de horno de arco eléctrico, que tiene en cuenta la naturaleza no lineal y la impedancia variable que exhibe este tipo de carga. A partir de la ecuación diferencial no lineal que describe la característica estática voltaje-corriente del arco eléctrico, se establece una ecuación equivalente lineal que facilita el ajuste de las constantes del modelo, usando mediciones reales de voltaje y de corriente tomadas en la etapa más crítica de la operación del horno. Se muestra el procedimiento de ajuste de los parámetros del modelo usando regresión Bayesiana Lineal. Se presenta a través de gráficas, la relación entre los parámetros del modelo de la etapa determinista y el comportamiento de la varianza de las funciones de densidad de probabilidad Gaussianas a posterior con el número de datos usados para la calibración del modelo. La validación de los resultados obtenidos se realiza simulando el modelo con los parámetros estimados para luego comparar éstos con mediciones reales. Se ha utilizado un medidor de Flicker que cumple con el estándar CEI IEC 61000-4-15 para determinar la Sensación Instantánea de Flicker (IFL) de las fluctuaciones presentes en las formas de onda reales y simuladas de las corrientes del arco eléctrico. Adicionalmente, se presenta en una gráfica el contenido armónico real y simulado de las corrientes de fase generadas en el horno.
Palabras clave: Horno de arco, oscilador de Chua, inferencia Bayesiana.
ABSTRACT
In this paper, the authors present the calibration of the parameter of arc furnace that considers the non-linearity and high variability of this type of load. Starting with a nonlinear differential equation that describes the voltage-current characteristic of the arc, an equivalent linear equation that simplifies the estimation of the original model parameters is proposed. Parameter estimation is then accomplished using Bayesian linear regression using measurements taken during the furnance’s most critical operation point. Relationships between the estimated value for the parameters and their uncertainty, in terms of the number of observations included in the model calibration process, are shown. Results obtained through simulation with the estimated parameters are contrasted against real data. A flicker meter, which complies with the IEC standard 61000-4-15, is used for determining the instantaneous flicker level (IFL) due to fluctuations present in the real and simulated current waveforms. Finally, the harmonic content of the real and simulated current waveforms is compared.
Keywords: arc furnace, Chua’s circuit, Bayesian inference.
INTRODUCCIÓN
El horno de arco eléctrico es conocido como el sistema más utilizado en las grandes industrias metalúrgicas para la producción de acero, aluminio, cobre y otros metales. El funcionamiento del horno de arco se divide en la etapa de fusión y en la etapa de refinado. La etapa de fusión se realiza a plena potencia y se complementa con energía auxiliar procedente de quemadores oxigas y lanzas de O2 para quemar los combustibles que pueda presentar la carga. Cuando la chatarra está totalmente fundida a unos 1600°C, el metal líquido se transporta al horno cuchara para ser sometido a un proceso de transformación denominado afino, donde se eliminan las impurezas y se agregan ferroaleaciones para ajustar la composición química del metal. Durante las dos fases del proceso de fundición, se observan caídas momentáneas de tensión (Flicker) en el barraje de conexión de la instalación o Point of Common Coupling (PCC) y en otros barrajes aledaños [1], en particular se hacen más severas durante la fase de fusión debido a que piezas de la chatarra que se funden cortocircuitan continuamente los electrodos del horno.
El efecto Flicker, también conocido como efecto parpadeo, puede originar molestias visuales en las instalaciones de iluminación dependiendo de su frecuencia y amplitud [2]. Otro problema que genera el horno de arco, para las redes de distribución, es la inyección de corrientes armónicas, que se originan por la naturaleza no lineal del fenómeno asociado al arco eléctrico, posibilitando la operación indeseada de los equipos conectados a la red de distribución y en las instalaciones eléctricas de usuarios aledaños. Operadores de red y usuarios de este tipo de carga conocen estos inconvenientes y en consecuencia, deben generar estrategias para su mitigación; como por ejemplo, el empleo de modelos matemáticos de horno arco que permitan predecir los impactos en la calidad de la energía del sistema de distribución que tendrían nuevas instalaciones, o evaluar el desempeño de sistemas de compensación como el D-StatCom (Distribution Static Compensator) o el SVC (Static Var Compensator) para instalaciones ya existentes [3].
Varios modelos matemáticos se han propuesto para el horno de arco eléctrico. En [4] se presenta un modelo que requiere las formas de onda reales de los voltajes y las corrientes del arco eléctrico. El modelo consiste en una resistencia variable en serie con una inductancia, junto con varias fuentes de corriente en paralelo para generar algunos armónicos que presentan las corrientes del arco eléctrico reales. La desventaja que tiene este planteamiento es que requiere de una cantidad masiva de datos para determinar los valores de funcionamiento de los elementos del modelo. Un enfoque con un modelo oculto de Markov para modelar el arco eléctrico se presenta en [5]. El modelo requiere muestras aleatorias de las señales reales de voltaje y corriente del arco eléctrico por fase en varios ciclos de funcionamiento, para generar diferentes puntos de operación sobre la curva voltaje – corriente con un valor de probabilidad relacionado con el modelo oculto de Markov. El modelo interactúa con el sistema eléctrico de potencia a través de fuentes de voltajes controladas por corriente. El modelo se valida usando datos reales.
Uno de los problemas que resulta del uso de estos modelos matemáticos está relacionado con la sintonización adecuada de sus parámetros. Actualmente, se encuentran en la literatura varios modelos para el horno de arco que tienen en cuenta las fluctuaciones en las formas de onda de voltaje y corriente del arco eléctrico, donde la sintonización de sus parámetros se realiza de forma heurística[6], o con base en gran cantidad de mediciones de voltajes, corrientes, Índices de Severidad de Flicker de Corta Duración (PST) de hornos existentes [7], o con base en curvas que muestran el comportamiento del factor de potencia real en este tipo de instalaciones [8]. En [9], se presenta una metodología para calibrar algunos de los parámetros del modelo propuesto en [10], usando estimación por máxima verosimilitud, en el que no es posible establecer la incertidumbre sobre los valores obtenidos en los parámetros. En [11], se utiliza una red neuronal para estimar todos los parámetros del modelo propuesto en [10], donde el conjunto de datos de entrenamiento se ha generado usando simulación.
Sin embargo, ninguna de las técnicas utilizadas para estimación de parámetros aplicadas a modelos de horno de arco tiene en cuenta algún tipo de incertidumbre sobre los parámetros. En este documento, se muestra una metodología para la sintonización automática de los parámetros del modelo de horno de arco presentado en [10], usando inferencia Bayesiana [12], teniendo en cuenta el nivel de incertidumbre sobre los parámetros del modelo que se estiman.
La sintonización de los parámetros se realiza con datos reales tomados en el ciclo de fusión del horno de arco [13]. Las señales que se utilizan son las formas de onda de los voltajes de fase y las corrientes del arco eléctrico en el secundario del transformador que energiza los electrodos del horno, muestreadas a una frecuencia de 2048 muestras por segundo. El modelo del horno de arco trifásico se ha realizado en el programa Pscad®, y el algoritmo de regresión Bayesiana lineal se ha implementado en Matlab®. La validación de los resultados se realizada comparando inicialmente los valores eficaces de las señales modeladas y reales. Luego se presenta una comparación de la Sensación Instantánea de Flicker (IFL) de las tres corrientes del arco, usando el flickermeter descrito en [14]. En los resultados obtenidos se compara el espectro armónico de las formas de onda de las corrientes de arco reales y simuladas. Finalmente, se presentan algunas conclusiones.
1. MATERIALES Y MÉTODOS.
1.1. MODELO MATEMÁTICO DEL HORNO DE ARCO.
En este trabajo se utilizó el modelo presentado en Alzate et al [10]. En resumen, el modelo se divide en dos partes, inicialmente se determina la característica estática no lineal entre el voltaje y la corriente del arco eléctrico y luego se considera el comportamiento dinámico del arco eléctrico modulando en amplitud el radio del arco eléctrico con tres señales: Una señal sinusoidal de baja frecuencia [15], una señal caótica de baja frecuencia generada con el oscilador de Chua [16]-[17] y una señal aleatoria con distribución de probabilidad Gaussiana.
El comportamiento determinista se obtiene resolviendo la siguiente ecuación diferencial Acha et al [18],
donde r es el radio del arco, i es la corriente instantánea del arco en amperios y kn (n=1,2,3), son las constantes del modelo que se desean estimar. El comportamiento dinámico del arco se obtiene generando un comportamiento de tipo aleatorio a la variable de estado r, para esto esta variable se modula en amplitud con las tres señales mencionadas anteriormente, lo que se describe matemáticamente como:
donde f es la frecuencia de las variación sinusoidal, ms, mg y mc son los índices de modulación de amplitud sinusoidal, aleatorio y caótico respectivamente, gn es una señal aleatoria con distribución de probabilidad normal y ch es una señal caótica en la banda de frecuencias de 3 a 25 Hz. Luego, el voltaje instantáneo del arco v en voltios, se determina a partir de la siguiente ecuación,
donde R es la resistencia del arco en ohmios. Este voltaje se incluye al sistema de potencia a través de una fuente de voltaje controlada “Single Phase Voltaje Source Model” de la librería de fuentes de voltaje de PscadTM. Para ajustar el factor de modulación ms, y la frecuencia de modulación f se requieren mediciones reales de voltajes y corrientes del arco eléctrico para cada fase. Con relación a los índices de modulación mg y mc, se han seleccionado heurísticamente valores diferentes para las tres fases con el objetivo de introducir desbalances en los voltajes del horno, y sus valores son proporcionales al PST medido en los nodos superiores del circuito del horno de arco. En la Tabla 1, se presentan los valores de los índices de modulación empleados.
El circuito eléctrico que conecta el horno de arco se basa en la topología presentada en [9]. En la Figura 1, se muestra el circuito implementado en PSCADTM.
1.2. REGRESIÓN BAYESIANA LINEAL
Considerando el modelo matemático del horno de arco dado por la ecuación , se propone estimar los parámetros k1, k2 y k3 por medio de regresión Bayesiana Lineal a partir de los datos reales tomados del comportamiento del horno de arco. La ecuación que describe el modelo del horno de arco se puede transformar a un modelo de regresión lineal, como se describe en Marulanda et al [9], y que consiste en una combinación lineal de las variables de entrada.
En el modelo de regresión lineal, las observaciones z1, z2,…, zm se relacionan con la función y(w,x) a través de la expresión:
donde e representa el ruido presente en las observaciones y explica cómo las mismas se alejan o acercan al valor del modelo. En lo que sigue asumimos que ε sigue una función de densidad Gaussiana, ε ∼N (0, β-1), donde b se conoce como la precisión.
Dados los coeficientes w0, w1, …, wm, la variable zi sigue una función de densidad Gaussiana,
donde wT = (w0, w1, …, wn). En el análisis de regresión clásico, se asume que las observaciones son independientes e idénticamente distribuidas (IID-Independent and Identically Distributed), luego
donde z es el vector aleatorio que contiene todas las observaciones, es decir zT = (z1, z2, …, zm) y N es el número de observaciones. La ecuación se conoce como la función de verosimilitud. Un método convencional para estimar los parámetros w consiste en encontrar los valores del vector w que maximizan el logaritmo de la función de verosimilitud, log p(z/w). Este criterio de estimación se conoce como Estimación por Máxima Verosimilitud (EMV) y equivale al criterio de mínimos cuadrados en el caso Gaussiano.
La EMV es un tipo de estimación puntual, en el que no es posible establecer la incertidumbre sobre el valor obtenido de los coeficientes w. La estimación Bayesiana, por el contrario, asigna una función de probabilidad a priori a los coeficientes w, que actualiza a través de la función de verosimilitud para producir una estimación de los parámetros que tenga en cuenta la incertidumbre de los mismos. La función de probabilidad actualizada para los parámetros w se obtiene empleando el teorema de Bayes,
donde p(w/z) es la función de probabilidad a posteriori y p(z) se conoce como la evidencia. Como la función de verosimilitud es una función cuadrática en w, una opción natural para la función de probabilidad a priori, p(w), es de nuevo una función cuadrática en w, de manera tal que la función de probabilidad a posteriori puede calcularse fácilmente. En particular, asumimos que la función de probabilidad a priori para w sigue la forma p(w)=N(w/0,α-1I), donde I es la matriz identidad y α es la precisión de los parámetros w. Se puede demostrar [12] que la función de probabilidad p(w/z) está dada como:
donde mN = bSNXTz, SN-1= XTX y X es una matriz cuyas filas están dadas por xiT, para 1< i <. Con esta función de probabilidad p(w/z) es posible calcular la función de probabilidad predictiva para un nuevo valor de salida z*, dado un nuevo valor de entrada x* [12],
Donde σN2(x*)=β-1+x*T SNx*.
Para emplear las expresiones anteriores en la práctica, es necesario estimar los valores de α y β. La inferencia Bayesiana en este caso consistirá en asumir funciones de probabilidad a priori p(α) y p(β), para luego marginalizar estas variables en la función a posterior p(w/z) y en la función predictiva p(z*/z, x*). Por simplicidad, asumimos que las variables α y β actúan como parámetros y usamos EMV para encontrar sus valores.
En este caso la función de verosimilitud que se emplea es la función de evidencia p(z), y la función a maximizar con respecto a α y β es el logaritmo ln p(z),
La maximización de la expresión anterior con respecto a α y β lleva a las siguientes ecuaciones de re-estimación para estas variables [12],
donde γ = ∑mi = 1 λi / (α + λi) y λi, para 1 ≤ i ≤ m, son los valores propios de la matriz βXTX. Los detalles de estas derivaciones pueden encontrarse en [12].
1.3. BASE DE DATOS
Los datosque se emplean para estimar los parámetros del modelo de horno de arco fueron usados por Cano et al [13], y consisten en mediciones reales de los voltajes de fase medidos en el secundario del transformador T2 y las corrientes del arco eléctrico durante 5 ciclos, con frecuencia fundamental de 50 Hz y frecuencia de muestreo de 2048 muestras por segundo, por lo que es necesario determinar inicialmente el voltaje del arco en cada fase, de acuerdo a los requisitos dados por la ecuación (1).
1.4. ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO.
Como se mencionó anteriormente, uno de los problemas fundamentales para el empleo de este modelo descrito en la sección 1.1, está relacionado con la sintonización de los parámetros kn con n = {1,2, 3}, para una aplicación específica. En esta sección, se muestra una metodología para determinar los mismos con base en mediciones reales. Para este trabajo, se tienen muestras de las formas de onda de los voltajes de fase en el secundario del transformador T2 y las corrientes del arco eléctrico. Los voltajes del arco eléctrico se obtienen a partir de la corriente del arco y el voltaje de fase en el secundario del transformador T2 como:
donde Rbaja y Lbaja corresponden a los parámetros del circuito de baja tensión del horno de arco.
Usando el desarrollo matemático que se presenta en Marulanda et al [9], se puede transformar la ecuación en una ecuación lineal equivalente, en términos de los parámetros kn que a la vez permite obtener un modelo de regresión lineal para el cálculo de las constantes kn de la ecuación . La ecuación lineal que resulta es de la forma:
donde u es una variable auxiliar. Realizando las siguientes sustituciones en la ecuación anterior: a=k1k3, b=k2k3, y=vi, x1=u2y x2=u(du/dt), se obtiene una ecuación lineal para el cálculo de los coeficientes a y b,
que se puede expresar como un modelo de regresión lineal, añadiendo ruido Gaussiano al modelo, de la forma:
donde w es el vector de parámetros [a b]’, x es el arreglo de los datos de entrada [x1 x2]’ de dimensión 2×N con N igual al número de observaciones o muestras de la corriente del arco, ε es el ruido Gaussiano aditivo y z es el arreglo del producto de las observaciones vi de dimensión N×1.
El cálculo de la derivada de u para determinar x2, definido como u(du/dt), se puede realizar de diferentes maneras, por ejemplo, utilizando la definición de la derivada de una variable discreta o expresar la variable u como una combinación lineal de funciones base para realizar su derivada de manera analítica. En este trabajo se determina la derivada de u expresando primero la variable como una combinación lineal de funciones base [12], es decir:
donde Φi (i = 1,…j) representan el conjunto delas funciones base y Ki (i = 1,…j) son los parámetros de ajuste o pesos de las funciones base. Para funciones base Gaussiana, la expresión matemática de Φi (i-ésima función base) está dada por:
donde μi es el centro de la i-ésima función base y s es un factor de escala. Para cada una de las fases, se resuelve w en la ecuación , tal como se explicó en la sección 1.2. Una vez conocidos los valores de a y b dados por el vector de parámetros w, se debe fijar un valor en alguna de las constantes kn del modelo para determinar las demás constantes. Por conveniencia, se ha elegido dar un valor particular a k3 ya que es común a los parámetros a y b. La aplicación de la metodología utilizada para determinar los parámetros del modelo se resume a continuación.

2. RESULTADOS Y ANÁLISIS.
En esta sección se presentan los resultados obtenidos en simulación del ajuste de los parámetros del modelo de horno de arco y la comparación de estos resultados con mediciones reales. El ajuste de las constantes kn, se ha realizado calculando la derivada de cada una de las corrientes del horno de arco eléctrico usando las ecuaciones y , (A través de funciones base Gaussianas), tomando el 85 % de los datos, 90 funciones base y un factor de escala de 0.001. En las Figuras 2 y 3 se muestran las formas de onda de la corriente del arco eléctrico para la fase a, real y sintetizada con funciones base Gaussianas.
En la Figura 4, se muestra la variación de las constantes k1n donde n = {a,b,c} (Modelo trifásico) en función de k3, en el intervalo de [1, 50] correspondiente a valores típicos [6].
En la Figura 4 se observa que la constante k1 para las fases a y b presenta un comportamiento similar con la variación de k3; sin embargo, la constante k1 para la fase c presenta valores menores respecto a los de las otras fases. Esto se debe principalmente a las diferencias que presentan las formas de onda reales de tensión y corriente del arco eléctrico de la fase c, respecto a las demás fases. Además, se observa en la gráfica que un aumento en la variable k3 debe ser compensado con la reducción en los valores de las otras dos constantes. Una característica similar para las constantes k2n en función del parámetro k3 se muestra en la Figura 5.
Con base en los resultados obtenidos, se realiza la simulación del modelo del horno de arco con los parámetros que se indican en la Tabla 2, que en promedio presentan el mínimo error para todas las señales de voltaje y corriente.
En las Figuras 6 a la 11 se muestran 5 ciclos de las corrientes del arco eléctrico, reales y simuladas, en el intervalo donde las señales presentan mejor aproximación.
Una comparación similar se ha realizado para las formas de onda de los voltajes de fase en el secundario del transformador T2 que se indica en la Figura 1.
En las anteriores Figuras se observa que el modelo del horno de arco captura la naturaleza no lineal de las corrientes y voltajes reales del arco, además, los valores obtenidos para las constantes kn usando regresión Bayesiana Lineal permiten obtener amplitudes de corrientes y voltajes similares a las de las señales reales.
Se determina el valor eficaz de las señales (Reales y simuladas) de tensión y corriente para cada una de las fases y se compararon los resultados de simulación con el respectivo valor eficaz de la señal real. El porcentaje de error se determina por medio de la siguiente ecuación, que muestra el error mínimo de estimación con respecto al valor real.
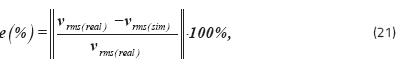
Con base en lo anterior, los errores obtenidos fueron 1.591 % para la fase a, 0.605 % para la fase b y 6.075 % para la fase c. Respecto a los voltajes se obtuvieron los siguientes resultados, 1.535 % para el voltaje de la fase a, 7.307 % para el de la fase b y 17.748 % para el de la fase c.
El Nivel Instantáneo de Flicker (IFL) que se denota con la letra S, es una medida de la cantidad de sensación de Flicker producida por fluctuaciones presentes en una señal de tensión (o corriente que circula por una resistencia de 1 Ω). Este parámetro tiene en cuenta la sensibilidad del ojo humano respecto a la frecuencia de cambios de la luminosidad de una lámpara incandescente [14]. En las Figuras 12 a la 14, se muestra una comparación de la evolución del IFL producida por las fluctuaciones presentes en las corrientes (Reales y simuladas) del arco eléctrico.
Debido a que el horno de arco es por naturaleza una fuente de armónicos, el modelo debe reproducir en forma cercana los armónicos generados por el arco. La Figura 15 muestra el espectro armónico de las corrientes del arco eléctrico medida y simulada para la fase a.
Se observa que las dos curvas presentan un comportamiento similar, produciendo componentes inter-armónicas y armónicas de orden par e impar. Resultados similares se obtuvieron para las corrientes de las demás fases.
Discusión: Estimación de la derivada usando la ecuación para variable discreta.
Los resultados anteriores se obtuvieron usando funciones base Gaussiana para estimar analíticamente todas las derivadas involucradas en el proceso. El cálculo de la derivada de una señal discreta x se indica en la siguiente ecuación:
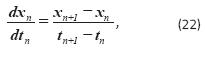
Al estimar las derivadas usando la ecuación y ajustar los índices de modulación de amplitud con los valores que se muestran en la Tabla 1, se obtuvieron los siguientes valores para las constantes kn (n = a, b, c) que en promedio presentan el mínimo error para todas las señales de corriente.
Simulaciones realizadas con el modelo, usando los valores que se muestran en la Tabla 1 y en la Tabla 3, muestran que los errores porcentuales de los valores eficaces de las señales de voltaje y corriente se incrementaron. Para las corrientes, los errores obtenidos fueron 16.70 % para la fase a, 4.34 % para la fase b y 14.5 % para la fase c. Respecto a los voltajes, se obtuvo un error de 7.11 % para la fase a, 4.34 % para la fase b y 14.50 % para la fase c.
3. CONCLUSIONES
La comparación de los resultados obtenidos a partir de las simulaciones realizadas con las medidas de una instalación, permiten inferir que el modelo implementado refleja el comportamiento caótico y aleatorio de la carga y valida su inclusión en los problemas que se van a analizar en la red de distribución. Además, el modelo puede ser utilizado para evaluar el desempeño de sistemas de compensación como el D-StatCom o el SVC y generar un concepto en cuanto a la operación de éstos y la viabilidad o no de su utilización para mitigar las perturbaciones. Basados en los resultados obtenidos, se puede concluir que la regresión Bayesiana Lineal junto con la estimación de derivadas con funciones base Gaussiana, aplicada a la sintonización de los parámetros de la primera etapa del modelo del horno de arco, entregan resultados aproximados a las mediciones reales.
REFERENCIAS
[1] M. F. Alves, Z. M. Assis Peixoto, C. Peixoto García y D. Goncalves Gomes, [2010]. An integrated model for the study of flicker compensation in electrical networks. Electric Power Systems Research, n° 80, pp. 1299-1305.
[2] H. Chong, Z. Yang, B. Chen, A. Huang, B. Zhang, M. Ingram y A. Edris, [2007]. Evaluation of Cascade-Multilevel-Converter-Based STATCOM for Arc furnace Flicker Mitigation. IEEE Transactions on Industry Applications, vol. 43, n° 2, pp. 378-385.
[3] A. García Cerrada, G. P. García, R. Collantes, T. Gómez y J. Anzola, [2000]. Comparison of Thyristor Controlled Reactors and Voltaage-Source Inverters for Compensation of Flicker Caused by Arc Furnaces. IEEE Transactions on Power Delivery, vol. 15, n° 4, pp. 1225-1231.
[4] M. Gol, S. Ozgul, B. Alboyaci, B. Mutluer, I. Cardiric y M. Ermis, [2010]. A new field data based EAF model for power quality studies. IEEE Transactions on Industry Applications, vol. 46, n° 3, pp. 1230-1242.
[5] M. Torabian y B. Vahidi, [2012]. A new stochastic model of electric arc furnace based on hidden markov model: A study of its effects on the power system. IEEE Transactions on power delivery, vol. 24, n° 4, pp. 1893-1901.
[6] O. Ozgun y A. Abur, [2002]. Flicker study using a novel arc furnace model. IEEE Transactions on power delivery, vol. 17, n° 4, pp. 1158-1163.
[7] R. Collantes y T. Gómez, «Identification and modelling of a three phase arc furnace for voltage disturbance simulation, [1997]. IEEE Transactions on Power Delivery, vol. 12, n° 4, pp. 1812-1817.
[8] R. Horton, A. Haskew y R. Burch, [2009]. A time-domain ac electric arc furnace model for flicker planning studies. IEEE Transactions On Power Delivery , vol. 24, n° 3, pp. 1450-1457.
[9] J. Marulanda, C. Sepúlveda and M. Álvarez, [2012]. Estimación de los Parámetros de un Modelo de un Horno de Arco Eléctrico Usando Máxima Verosimilitud. TecnoLógicas, vol. 29, pp. 69-89.
[10] A. Alzate Gómez, J. Marulanda Durango y A. Escobar Mejía, [2010]. Electric arc furnace modeling for power quality analysis. Bogotá: En: IEEE Conference of the Andean Council ANDESCON.
[11] C. Henao Baena, J. Marulanda Durango y M. Álvarez López, [2013]. Calibración de los parámetros de un modelo de horno de arco eléctrico empleando simulación y redes neuronales. En: proceso de publicación.
[12] C. Bishop, [2006]. Pattern recognition and Machine Learning, Cambridge: Springer.
[13] E. Cano and E. Tacca, [2005]. Arc furnace modeling in ATP-EMTP. Montreal, Canada: Presented at the International Conference on Power Systems Transients.
[14] C. I. P. 61000-4-15, [1997]. Flickermeter-Functional and Testing Specifications. CEM Basic EMC Publication.
[15] G. Manchur, [1992]. Development of a model for predicting flicker from electric arc furnace. IEEE Transactions on Power Delivery, vol. 7, n° 1, pp. 416-426.
[16] M. Kennedy, [1993]. Three steps to Chaos-Part I: Evolution. IEEE Transactions on circuit and systems-I: Fundamental, theory and applications, vol. 40, n° 10, pp. 640-665.
[17] M. Kennedy, [1993]. Three steps to chaos-Part II: A chua's circuit primer. IEEE Transactions on circuit and systems-I: Fundamental, theory and applications, vol. 40, n° 10, pp. 657-674.
[18] E. Acha, A. Semlyen y N. Rajakovic, [1990]. A harmonic domain computational package for nonlinear problems and its application to electric arcs. IEEE Transactions on Power Delivery, vol. 5, n° 3, pp. 1390-1397.