http://dx.doi.org/10.18359/ravi.1707

Artículo
Revista Academia & Virtualidad 9(1): 24-40, 2016

Aprendizaje de la matemática, una condición necesaria para el aprendizaje de la física inicial a nivel superior¹

Óscar Jardey Suárez²
Fundación Universidad Autónoma de Colombia, Colombia

Recibido, noviembre 17 de 2015
Concepto evaluación, diciembre 24 de 2015
Aceptado, enero 27 de 2016

Resumen

Este documento es consecuencia del avance de investigación que pretende estudiar la afirmación que dice que el “[…] aprendizaje de la matemática como una condición necesaria, pero no suficiente, para el aprendizaje de la física”. La metodología de la fase inicial de la investigación es cualitativa, basada en una revisión documental y se enfoca en establecer los avances y dificultades en el estudio de la comprensión de la noción de variable en la educación matemática y su uso e implicaciones en el contexto de la física. Los resultados señalan la importancia de lograr una alta comprensión de la noción de variable manifiesta en un razonamiento algebraico necesario para el aprendizaje de la física. Entre las reflexiones está la “homografía física”, como un elemento que complejiza la comprensión de la noción de variable en su paso del contexto matemático al físico, así como la necesidad de lograr una comprensión aceptable de la noción de variable, en particular de los objetos matemáticos como función afín parabólica para el inicio del estudio de la física en la Educación Superior.

Palabra clave: didáctica de la física, noción de variable, cinemática, objeto matemático.

Learning Math, a required condition for learning top-level basic physics

Abstract

This paper is a partial result of research aimed to study a claim, which says “that [...] learning mathematics as something necessary but not sufficient condition for learning physics.” The methodology of the initial phase of the research is qualitative and based on a literature review focused on establishing advances and difficulties to understand the concept of variable for learning mathematics and the relevant use and implications upon the context of physics. Results point out the relevance of achieving a high level to understand the concept of variable involved in an algebraic reasoning necessary for learning physics. Among the considerations we have a “physics homograph” as a complex issue to understand the variable concept to work from math to physics context as well as a need to achieve a suitable understanding of the variable concept, particularly with math objects, as a parabolic affine function to begin the study of physics in higher education.

Keywords: teaching physics, variable concept, kinematics, mathematical object.

Aprendizado da matemática, uma condição necessária para o aprendizado da física inicial a nível superior

Resumo

Este documento é consequência do avance de pesquisa que pretende estudar a afirmação que fala que o “[...] aprendizado da matemática como uma condição necessária, mas não suficiente, para o aprendizado da física”. A metodologia da fase inicial da pesquisa é qualitativa, baseada numa revisão documentaria e enfoca-se em estabelecer os avances e dificuldades no estudo da compreensão da noção de variável na educação matemática e seu uso e implicações no contexto da física. Os resultados sinalam a importância de atingir uma alta compreensão da noção de variável manifesta num razoamento algébrico necessário para o aprendizado da física. Entre as reflexões fica a “homografia física”, como um elemento que dificulta a compreensão da noção de variável no seu passo do contexto matemático ao físico, tanto quanto a necessidade de atingir uma compreensão aceitável da noção de variável, particularmente dos objetos matemáticos função e afim e parabólica, para o início do estudo da física na educação superior.

Palavras chave: didática da física, noção de variável cinemática, objeto matemático.

Introducción

La formación en ciencias e ingeniería pasa por una crisis manifiesta en los resultados de pruebas estandarizadas, así como en la cantidad de estudiantes que seleccionan e inician sus estudios en estas áreas (Fourez, 2005; Gil et al., 2005). Los hechos anteriores son objeto de estudio por diversas áreas del conocimiento que tienden a buscar comprender e interpretar las razones que han llevado a este estado a la sociedad para poder aproximarse a transformarla. Por ejemplo, en el análisis de las pruebas PISA del año 2012, se encuentra que en Latinoamérica el porcentaje de estudiantes con nivel alto es bajo, apenas Uruguay alcanza 1.3%, México 0.6% y Colombia el más bajo con 0.3% (Soledad Bos, Ganimian, & Vegas, 2014a); de otro lado, los reportes de matemáticas indican cómo algunos estados de México logran los mejores resultados de la región, así como otros estados alcanzan los peores resultados de la región; sin embargo, en el global se dice que México es, junto con Chile, el que tiene mejores resultados en matemáticas (Soledad Bos, Ganimian, et al., 2014a). Al observar específicamente las áreas de matemáticas y ciencias, se evidencia que en México está dos años atrás del promedio de los países de la OCDE, si bien ha mejorado en su rendimiento en matemáticas su tasa de crecimiento es muy baja al punto que demoraría 28 años en llegar a la media de los países de la OCDE, en tanto que en ciencias su desempeño no ha variado y es muy similar a matemáticas (Soledad Bos, Ganimian, & Vegas, 2014b). El caso en Colombia es un tanto más crítico, pues el nivel de desempeño bajo se presenta en un gran porcentaje en la población estudiantil (7 de 10 frente a 2 de 10 de la OCDE en matemáticas) en ciencias 6 de 10 están en los niveles bajos frente a ninguno en los países de la OCDE; lo anterior es un panorama difícil del sistema educativo colombiano (Soledad Bos, Ganimian, Vegas & Horacio Álvalrez, 2014).

Para efectos de analizar algunos aspectos de los estudiantes que inician sus estudios en el área de la ingeniería que involucran el estudio de la física, es preciso considerar, de un lado, los elementos en la formación de ingenieros, entre los que se destaca las ciencias y las matemáticas, como bien lo señala Callaos (2010) cuando revisa el currículo de ingeniería en perspectiva y propositivamente, como uno de los tres pilares en la formación de ingenieros; desde otro punto de vista, se identifica que “el puente está quebrado” entre la Educación Media y la Educación Superior (V. Gómez, 2006), lo que se evidencia en las dificultades para dar el salto, por razones económicas, sociales y principalmente cognitivas, en este panorama las matemáticas ni la física son ajenas a la situación, éstas son áreas de interés estructural en la formación de ingenieros junto con la techné y la praxis.

Para entrar en el objeto de estudio es preciso retomar la discusión de los que algunos han denominado el pensamiento variacional (Cantoral & Farfán, 2013; Vasco, 2009-2010) aproximando a entenderlo como la capacidad para darle sentido a las funciones numéricas y manejarlas de manera flexible y creativa, para entender, explicar y modelar situaciones de cambio, con el propósito de analizarlas y transformarlas (Castiblanco, Urquina, & Acosta, 2004), que para el caso del actual trabajo acotaremos esta conceptualización a la idea de razonar algebraicamente como esa capacidad de utilizar la noción variables conscientemente de sus características y las implicaciones en sus uso en diversos contextos; esta forma de razonamiento hace parte de un razonamiento científico que se ajusta en una epistemología propia de las ciencias, en la que se entiende por ejemplo que la matemática es básica en el avance de la física; entendiendo la didáctica como “epistemología aplicada” el razonamiento algebraico es necesario en la idea de formar o potenciar el razonamiento físico.

Los trabajos, en la educación matemática, tendientes a fortalecer la noción de variable, en diferentes momentos, retoman en un porcentaje significativo los fenómenos físicos como contexto de análisis, por ejemplo el uso de la cinemática unidimensional uniforme (Miranda, Radford, & Guzman, 2013), allí se nota que los contextos son un ente de mediación, mas no son objeto de estudio, es decir no se articulan a la didáctica de la física sino se centran en el objeto matemático de estudio, en tanto que los estudios en física se centran en el estudio de los diferentes conceptos físicos (que podríamos llamar variables) en relación con su dominio y relación con las otras variables físicas para poder interpretar, entender, explicar y predecir los fenómenos o eventos de la naturaleza o de la “realidad”, dando por sentado el conocimiento de los objetos matemáticos; sin embargo, existe la conciencia entre los profesores de física de la claridad de las limitaciones de los estudiantes en relación con el manejo matemático (Redish, Steinberg, & Saul, 1996; Steinberg, 1997; Steinberg, Saul, Wittmann, & Redish, 1996) (aritmético, geométrico y álgebra) que impiden apropiar algunos conceptos físicos, como la cinemática en cursos iniciales de física para ingenieros (Bastién, Mora Ley, & Sánchez, 2010).

La identificación de los problemas aritméticos, geométricos y algebraicos, en general clasificados en obstáculos epistemológicos y didácticos, para abordar situaciones problemas hipotéticas o reales de orden físico (Bastién et al., 2010), llevan implícito el reconocimiento de la variable en el contexto matemático, la que se ha venido estudiando en la educación matemática (Maury Mancilla, Palmezano Sarmiento, & Cármaro Barrios, 2012; Trigueros, Reyes, Ursini, & Quintero, 1996; Vega & Borges Cuesta, 2012; Villa Ochoa, 2011) y que se tiende a tratar el objeto matemático como único objeto de estudio, apoyado en diversos contextos algunos de los cuales son de orden físico.

En este sentido la forma en cómo se usa la variable en física, corresponde en alguna medida, coincide en cómo se concibe la variable en el contexto de la educación matemática, específicamente cuando se usa como incógnita, como número generalizado o como relación funcional (Ursini & Trigueros, 2006), la que se complejiza más en el estudio de la física, cuando las letras no solo denotan las variables o conceptos físicos, sino también constantes de orden general, asumen roles distintos dependiendo del contexto entre otros (Steinberg, 1997).

La matemática, vista como herramienta de la física (Krieger, 1997, 1998), es un elemento que puede tener consecuencias de éxito o fracaso en el estudio de la física a nivel superior, en particular, la noción de variable (desde la matemática) asociada al contexto de la física inicial (posición, velocidad, aceleración, fuerza,…) en carreras de ingeniería guardan una estrecha relación, tal y como lo plantea Ursini y Trigueros (2006), en razón a que en el desarrollo del estudio de los contenidos en cinemática, por ejemplo la posición, pueden ser una incógnita cuando se indaga en una situación problema de manera específica, pero también puede tener una relación funcional cuando se señala que “ ...la posición en función del tiempo…”, y a su vez puede ser número generalizado cuando se indica que “…la velocidad instantánea es la derivada de la posición…”, eso sin mencionar que podemos señalar condiciones iniciales donde la posición asume valores específicos y es preciso tratarla con subíndices para poder señalar cual es la posición en mención (inicial, final o en un punto específico).

En este trabajo se aborda el estudio desde el contexto de la educación matemática, pasando a los conceptos iniciales estudiados en la física concluyendo y ejemplificando desde los contenidos como la matemática es un artefacto (Cole, 1999; Wartofsky, 1979) o mediación en el estudio de la física a nivel superior.

Metodología

La investigación busca identificar o hacer evidentes las relaciones existentes entre el aprendizaje de la matemática como condición necesaria para el aprendizaje de la física basado en una revisión bibliográfica. El desarrollo de la investigación marco se orienta principalmente por la pregunta ¿Qué efecto tiene sobre el nivel de aprendizaje de la cinemática unidimensional cuando se aporta información relacionada con el nivel de comprensión de variable? En relación con el proceso metodológico esta fase de la investigación es bibliográfica (Quintana, 2006; Rodriguez & Moya, 2008) y se centra en el rastreo de información proveniente de revistas, así como la revisión de textos de física seguidos a nivel superior en la facultad de ingeniería. Una premisa considerada en la clasificación y análisis de la información, es la competencia de mapeamiento informacional establecida por André, la cual conceptúa así: “…mapear un contenido significa sintetizarlo, lo que requiere una lectura atenta de las informaciones, su comprensión, la identificación de las ideas principales del autor y su registro escrito de modo conciso, coherente y objetivo…” (2009).

La sistematización de la información se hizo apoyado en Ms Excel ® y Atlas ti ®; en ellos se catalogó la publicación (título, palabras claves, año de publicación, dirección electrónica, tipo de publicación), y se procedió a identificar las ideas relevantes que se encontraron; aquí se clasifican primero la educación matemática y posteriormente los referentes físicos cerrando con algunos ejemplos que dan cuenta de la evidencia de la matemática como condición necesaria para aprender física.
El principal criterio para avanzar en la selección de la información es que hubiese sido publicada, preferiblemente, de los últimos siete años; aunque se evalúan otras fuentes con información relevante y que dan indicios claros de la persistencia en el objeto de estudio.

Resultados

Uno de los hallazgos es que la educación matemática esta parcelada (Pareja Heredia), al estilo de la teoría de Taylor (Bravo Carrasco, 2005), desde hace mucho tiempo dejando por fuera algunas áreas que contribuyen a dar coherencia. Se afirma que enseñar aritmética sin álgebra es reducir esa gran riqueza que ofrece este tipo de conocimiento a un asunto de orden mecánico y rutinario, es así como la aritmética, el álgebra y la trigonometría están segmentadas y desconectadas (Pareja Heredia), lo que de antemano es un factor, no controlable, en el paso de los estudiante por la educación antes de ingresar a la universidad.

La noción de variable

Ursini y Trigueros, profesoras en el campo de la matemática y la educación matemática, han venido estudiando la comprensión del concepto de variable (Trigueros et al., 1996) encontrando que hay un impacto positivo en la comprensión de ésta, en la medida en que el estudiante avanza en el desarrollo de su carrera a nivel de Educación Superior; sin embargo, cuando los estudiantes de cualquier nivel enfrentan problemas complejos acuden a la aritmética como herramienta básica en su desarrollo, en sus reflexiones finales consideran la necesidad de generar mayores oportunidades de reflexión de forma que se generen en ámbito cognitivo muchas posibilidades en el uso de la variable (Ursini & Trigueros, 2006). El estudio se ha basado, desde el punto de vista estadístico en la teoría de respuesta al ítem (TRI), ubicando situaciones problemas hipotéticas en el ámbito de las matemáticas diferenciadas según el nivel educativo al que se dirigen.

Escalante y Cuesta (2012) en una investigación referida a la comprensión del concepto de variable en la Educación Superior, en particular las licenciaturas en Economía y de Informática, basado en la contextualización de la noción de variable y la relación funcional con situaciones contextualizadas, encontraron que los estudiantes presentan dificultades cuando enfrentan lectura analítica, así como en el paso de diferentes representaciones de un mismo objeto matemático (lenguaje natural, aritmético, geométrico, lenguaje algebraico), lo que da indicios de que aún falta fortalecer el razonamiento algebraico.

Gómez (2007), en su tesis doctoral, indaga en relación con la forma en cómo se construye la noción de variable en niños de básica, a partir de experiencias con fluidos, concluye que los niños construyen la noción de variable cuando interactúan la centración, causalidad y la seriación en la percepción de fenómenos concretos. Este hecho es próximo a identificar la necesidad de la interacción del entorno con los objetos matemáticos, de manera dirigida, para que los menores construyan la noción de variable. En este trabajo se ubican experiencias de fluidos pero el enfoque de observación y construcción es meramente matemático.

Wagner (1983), al respecto, señala la dificultad existente por parte de los jóvenes en el estudio del álgebra, donde las letras tienen varios significados, como número o como expresión literal, o el caso de letras que identifican un número que no tiene una representación numérica (π), termina sugiriendo que los profesores incluyan de manera paulatina la noción de variable y la utilización de las letras en matemáticas.

Trabajos como el de Villa (2011) se enfocan en el estudio de temas como noción de derivada, usando Geogebra®, desde la razón de cambio, donde se evidencia la necesidad de reconocer, entender y comprender con anticipación la noción de variable (dependiente e independiente) y las relaciones que allí se presentan, esto coincide con la necesidad de ubicar un pensamiento variacional en el marco de un sistema variacional (Vasco, 2009-2010) que considera en una capa superior el cálculo, diferencial e integral (Cantoral & Farfán, 2013). Previamente, Villa y Ruiz (2010) estudiaron el razonamiento variacional como parte fundante de la propuesta antes expuesta, e inspirados en otros trabajos se aproximan al diseño de estrategias enfocados al estudio y desarrollo del razonamiento variacional, de las que manifiestan haber nuevas conjeturas para la enseñanza de algunos conceptos matemáticos.

El doctor Vasco a lo largo de su vida ha venido aportando en relación con la educación matemática, y en una de sus reflexiones relacionadas con la reestructurar la educación matemática en el contexto colombiano desde un enfoque sistémico, asume que el razonamiento variacional es el futuro en el área, pues pasar de un razonamiento aritmético a un razonamiento variacional permitirá un mejor desempeño de las personas en su vida de adulto ya sea en la Educación Superior o no (Vasco, 2009-2010), lo anterior al menos en el estudio de la física es fundamental.

El profesor Cantoral, reconocido investigador mexicano en el ámbito de la matemática educativa, participa de un proceso con la Secretaría de Educación de México que divide la enseñanza de la matemática en cinco segmentos en el que está el desarrollo del pensamiento y lenguaje variacional, del que menciona la ausencia de ideas en la Educación Media y Superior para su desarrollo (Cantoral & Farfán, 2013) coincidiendo con Vasco en este sentido.
Como categoría superior, entonces, se identifica el razonamiento variacional, la noción de variable (letra generalizada, incógnita, relación funcional), la letra como símbolo que representa algo, diversos contextos para mediar en el objeto de estudio entre los que la física, como el caso de los fluidos, les permite experimentar y tener una proximidad de interacción en la construcción de una noción abstracta, así como la resolución de problemas reales o hipotéticos como fin o medio para lograr el desarrollo de razonamiento en los estudiantes y, en general, en los individuos, la física ofrece una variedad de experiencias que permiten estudiar el concepto físico y afianzar el concepto matemático.

A manera de síntesis, los diversos trabajos han evidenciado la importancia de lograr en los estudiantes, en el tiempo, una mejor comprensión de la noción de variable como parte del razonamiento matemático requerido en la Educación Superior, y lo anterior se manifiesta cuando logran identificar sus usos y diferenciarlos en contextos específicos. Llegar al estado de comprensión expuesto, pues para estudiantes de diferentes edades y niveles educativos, resulta complicado, porque se presentan hechos visibles como ignorar la letra, no identificarla como número generalizado y más aún como relación funcional entre dos variables. Los hechos mencionados se agudizan en el paso de los semestres en estudiantes a nivel superior que requieren un razonamiento matemático basado en la noción de variable, en cuyo punto es donde la investigación se centra en conjunto con aquellos estudiantes que en su formación profesional requieren estudiar física como en el caso de la ingeniería.

La cinemática

Uno de los temas con mayor riqueza de estudio, en la física educativa, es la cinemática y la mecánica clásica. Allí se encuentran estudios variados que tienden a indagar desde las concepciones de movimiento, la noción de aceleración de la gravedad y, en general, todas las temáticas de la cinemática. Allí se proponen actividades y se aproximan a medir el impacto de dichas propuestas.

Por ejemplo, una actividad tipo tutorial orientada a la comprensión de gráficas en el movimiento unidimensional, soportada por el aprendizaje activo, arrojó que los estudiantes de física en carreras de ingeniería tienen su mayor dificultad en la noción de integral de área bajo la curva, y centró su intervención allí (Tejeda, 2009), al final de la cual encontró una mayor ganancia entre quienes participaron del desarrollo de la actividad tutorial, sin embargo enfatiza que ésta es susceptible de ser mejorada (Tejeda & Alarcón, 2012).

Alzugaray, Enrique y Esterkin (2014), a partir de situaciones problema, exploran conceptos y preconceptos de cinemática y dinámica de los estudiantes de un curso introductorio de física. Los resultados son desalentadores en la medida en que apenas 2.9% usa gráficas, 33.6% están fundadas en el modelo científico, y 23% usa las ecuaciones correctamente. En sus conclusiones demandan mayor interés de los investigadores, de los profesores en Educación Superior, señalando que los profesores y estudiantes deben reflexionar en conjunto para la resolución de problemas, así como la necesidad de fortalecer las estrategias didácticas.

Corona, Sánchez, González y Slisko (2012), a partir de un problema de cinemática, analizaron las preferencias elegidas en la solución y su nivel cognitivo de estudiantes de Básica Secundaria, Educación Media y estudiantes de la licenciatura en física, y encontraron que el nivel cognitivo juega un papel fundamental en la forma en cómo se aborda y organiza la solución de problemas.

Los anteriores trabajos coinciden con los planteamientos de Ursini y Trigueros (2006) en el sentido de profundizar en la reflexión de las situaciones problema, de afianzar y explorar la forma de abordar las situaciones aunque unas en el contexto de la física y otras en el contexto de las matemáticas. Bastién, Mora y Sánchez (2010) estudiaron los obstáculos presentes en los estudiantes al enfrentar un problema de cinemática elemental que provoca que haya bajo rendimiento académico. Como resultado del estudio clasificaron los obstáculos en: emplear sólo datos escritos (no se incluyen datos implícitos en el contexto del problema como “parte del reposo”), localización de ecuaciones en que aparece la incógnita y su utilización reflexiva (la estrategia datos fórmulas y solución genera que los estudiantes no discutan la solución por utilizar), el único camino (no se conciben las diferentes opciones en la solución de un mismo problema), el sistema de referencia fijo (los textos y el profesor refuerzan el hecho de un sistema de referencia y coordenadas fijo), la utilización de sistema de referencia propios (frente a dos o más móviles no se concibe que haya un solo sistema de referencia) y la falta de correspondencia entre matemáticas y física (no asocia cada una de las variables de la ecuación con su concepto físico). En sus conclusiones señalan que los obstáculos (epistemológicos y didácticos) no corresponden precisamente con la cinemática y dan especial interés a la metacognición lo que va dando mayor validez al estudio que actualmente se está proponiendo.

Entre tanto, Morales, Mena, Vera y Rivera (2012) identifican cuatro aspectos, cuando se abordan experimentos de cinemática, siendo éstos: la argumentación gráfica, rol del tiempo, funcionalidad de las gráficas y análisis variacional. Concluyen que el conocimiento matemático se construye y es utilitario, de tal manera que la fórmula no es el centro sino el proceso en el que la matemática y la física adquieren su sentido.

Se identifica entonces cómo el estudio de la física, en sus cursos iniciales, mantiene una relación de dependencia con el estudio de la matemática a nivel de aritmética, álgebra y algunos elementos de cálculo y que se profundiza al momento de resolver situaciones problemas hipotéticos o reales en los que intervienen no solamente el concepto físico sino los elementos matemáticos.

Otros trabajos en la didáctica de la física

En el estudio de la física se ha discutido con antelación las dificultades para el aprendizaje de ésta encontrando algunos orígenes relacionados con las dificultades en el entendimiento de la matemática, sin identificar con claridad cuál es el papel de uso y diferenciación de los objetos matemáticos en contextos específicos enmarcados por conceptos físicos.

Redish et al. (1996) reflexionaban y estudiaban la implicación de la comprensión de la diversidad en el uso de los símbolos, en la enseñanza y aprendizaje de la física que derivan en entender la matemática incorrectamente en el contexto de la física. Señalan (Redish et al., 1996) que en ocasiones los estudiantes pueden realizar operaciones en el contexto de la matemática, pero estas mismas en el contexto de la física ya no son realizables, quizá por no dar el significado correspondiente al símbolo. Cuando refieren símbolos como v,x₀,h,e,c,U_g,… , se está acudiendo a conceptos propios de la física con delimitaciones que suelen o pueden ser distintas de las especificadas por los objetos matemáticos en las que aparecen, en tanto que en matemática símbolos como x,y,z,r,π,ω,… son entidades abstractas con las que se hacen operaciones abstractas en el marco de uno o varios sistemas formales de inferencia o deducción (Wartofsky, 1973).

Cuando Redish et ál. (1996) desarrollan el trabajo de investigación identifican cómo los estudiantes fallan en: relacionar los símbolos usados en la medición más allá de números reales, considerar las variaciones asociadas, analizar las ecuaciones, comprender las ecuaciones como relaciones entre variables, coordinar espacio y tiempo e identificar las ecuaciones como representación de una realidad. Steinberg et al. (1996), en una investigación mixta (cualitativa y cuantitativa) realizada en un curso de segundo semestre de física con alto contenido de cálculo, identifican que los estudiantes requieren y presentan dificultades en una cantidad considerable, de conocimiento matemáticos clasificados en: gráficas, ecuaciones y vectores; los gráficos orientados a interpretar fenómenos físicos basados en representaciones gráficas, comprender los experimentos, leer gráficamente relaciones de orden cuantitativo, las ecuaciones dirigidas a entender la situación real o hipotética física y su representación a través de una ecuación así como la relación funcional entre variables y entender la noción de vector y las representaciones en diferentes sistemas de coordenadas, es decir que existe una complejidad matemática en el estudio de la física.

Steinberg, Wittmann y Redish (1996) en la búsqueda de soluciones al respecto, incursionaron en el desarrollo de tutoriales de física, idea inicialmente desarrollada por Lilian McDermont (Mcdermott, Shaffer, & Washington, 2002; Steinberg, Oberem, & Mcdermott, 1996; Steinberg, Wittmann, & Redish, 1996; Tejeda &Alarcón, 2012) y el grupo de investigación de la Universidad de Washington, en el contexto de las ondas, encontrando que mejoraba su comprensión y rendimiento de los estudiantes; la noción de tutorial parte de investigaciones previas que han identificado algunas dificultades de los estudiantes y que, en consecuencia, se abordan desde allí.

Algunos ejemplos de objetos matemáticos y su utilización en física

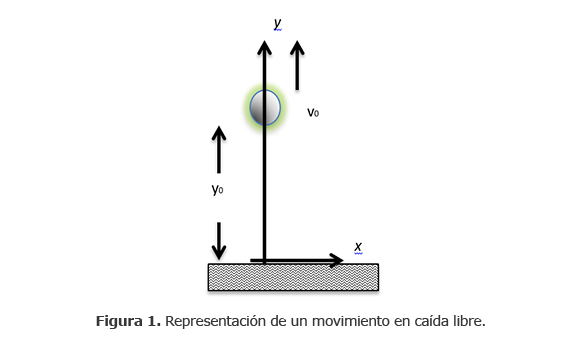
La caída libre como fenómeno físico específico en el que la aceleración de la gravedad g tiene un cierto valor dependiendo del lugar geográfico, y su condición en la dirección radial hacia el centro de la Tierra, es un evento físico en el que interactúan varias variables desde el punto de vista cinemático (tiempo, posición, velocidad, aceleración de la gravedad) (Resnick, Halliday, & Krane, 1996; Serway & Jewett, 2008) con características que permiten interpretar y predecir el movimiento de un objeto en posiciones cercanas a la superficie terrestre, el análisis y modelamiento del fenómeno físico en cuestión, ilustrado en la figura 1, se hace a través de los objetos matemáticos de funciones afín y parabólica en condiciones particulares.

Los objetos matemáticos, función afín y función parábola, son ampliamente estudiados en diversos textos de matemáticas de la educación básica, media y en los primeros cursos en las universidades; por ejemplo, Stewart et al. (2012) estudia la representación gráfica, la tablas de datos, las expresiones algebraicas así como los demás aspectos de estos objetos matemáticos.

En la figura 2 aparecen tres representaciones del objeto matemático función afín “gráfica, algebraica y tabulado”, con variable independiente y dependiente de manera general y abstracta x y y respectivamente, del mismo modo trata el objeto matemático función parábola (figura 3) analizando además su concavidad, mínimo, máximo, puntos de corte, etc.

La riqueza del estudio de estos objetos matemáticos son fundamentales para abordar el estudio del movimiento uniforme o movimiento uniformemente acelerado, esto sin inmiscuir aún la noción de derivada e integral, toda vez que se asume en condiciones ideales y bajo un sistema de referencia como el mostrado en la figura 1, cuya ecuación describe y predice la posición en función del tiempo del movimiento del objeto es y(t)= y₀+v_ot - gt²/2.

Por ejemplo, en el estudio del movimiento de una partícula bajo aceleración constante, se inmiscuyen los objetos matemáticos función afín y parábola, tal como se indica en la figura 4, en los que subyace las nociones de derivada e integral, y se señala la forma en cómo se relaciona la posición, la velocidad y la aceleración (en un movimiento con aceleración constante) y en los que interactúan los objetos matemáticos afín y parábola en el contexto particular de la cinemática ya mencionada.

Es así como en la tabla 1 se presenta la forma en cómo se presenta el primer teorema fundamental del cálculo y como se utiliza en uno de los contextos de la física, la cinemática; nótese que si bien en el contexto de la física, difiere de la formalidad matemática, subyacen las condiciones matemáticas y están ubicadas en un contexto específico.

En los anteriores ejemplos, entonces, se logra evidenciar una interdependencia entre los conceptos de la física y los de la matemática, pero hay que ver como este ejercicio se complejiza en el estudio de la física cuando los símbolos utilizados pueden tener diversas connotaciones, tales como un número (e,π ), una constante universal (c,h,k_e…), algunos parámetros experimentales (R,T,k_r...), unidades de medida (m,s,g,K,...), condiciones iniciales (x₀,y₀,…), variables dependientes (x,y,z,t,…), variables independientes (x,y,z,…), en las que se identifica una especie de homónimo en la escritura pero que el contexto específicamente indica la forma en cómo se debe interpretar o entender (Redish et al., 1996).

Conclusiones

En el estudio de la física las variables son conceptos (e.g. posición, velocidad, aceleración,…) sujetos a ciertas condiciones con las cuales asumen comportamientos explicando y prediciendo fenómenos físicos, pero necesariamente se acude a objetos matemáticos para su estudio, es decir que la matemática es una herramienta o artefacto mediacional entre la realidad estudiada y los conceptos físicos que permiten explicarla y a su vez predecirla, como el caso de un objeto en caída libre o el movimiento uniforme.

En general, los trabajos en el área de la educación matemática que estudian la noción de variable (en sus aspectos abstractos con características propias de ésta, su relación con los aspectos cognitivos, y se podría decir autocontenida en el área, separada de otras áreas o considerando algunas de ellas como subsidiarias, es decir es el estudio de la noción de variable desde sus propias construcciones en el área) acuden ocasional y parcialmente a otros contextos como subordinados para lo requerido. Esta relación no es objeto de discutir cuál es más importante, es decir que no es objeto de discusión de si la matemática es más importante que la física o la física es más importante que la matemática, o si la física es la aplicación de la matemática, o ésta es una herramienta de la física, lo cierto es que de la relación mutua se construye conocimiento.

Para la educación matemática, algunos eventos o fenómenos físicos son fértiles para el diseño de propuestas tendientes a favorecer la comprensión de la noción de variable y en consecuencia el razonamiento algebraico. Los objetos matemáticos, función afín y función parabólica, son muy útiles en el estudio de eventos físicos como el movimiento uniforme o uniformemente acelerado en una dimensión. Por ejemplo, la burbuja de agua en un frasco de vidrio largo después de un tiempo t, corto, se mueve con magnitud de velocidad constante, haciendo que la posición (x) en el tiempo (t) se observe como una recta (x(t)=vt+x₀), es decir, el experimento permite registrar datos de una recta y al representarlos en una gráfica se observa la línea recta, a la que se le puede hallar la ecuación y proceder a hacer interpolaciones, explicaciones y predicciones del movimiento de la burbuja.

Se han evidenciado entonces cuatro representaciones de los objetos matemáticos (verbal, tabulado, algebraico y gráfico) que se utilizan ampliamente en el estudio de la física con una interrelación y navegación entre cada una de ellas, tal como se hace en el análisis de los resultados de un laboratorio de física (Suárez & Hurtado, 2012a, 2012b; Suárez & Hurtado, 2013) en los que los datos se aproximan a modelos matemáticos a partir de métodos de regresión, o simple transformación de los datos para ajustarlos a una función afín, donde estas representaciones contribuyen en la comprensión de los fenómenos físicos.

En el estudio de la física hay una “homografía física”, que se entendería como el uso de un mismo símbolo para representar diferentes variables o constantes. Por ejemplo, µ se utiliza como prefijo para indicar un factor de 10-6, pero también se usa como densidad lineal cuando se estudian las ondas en una cuerda, y esto solo por mencionar dos de los usos del mismo símbolo con significado distinto constituye una muestra de las múltiples homografías que se presentan y que contribuyen a complejizar el estudio y conceptualización de los temas de física, así como los presentes en la noción de variable.

Revisada la información, reportada en diferentes documentos producto de investigaciones, se puede afirmar que se requiere exigir y apoyar fuertemente el estudio de la matemática cuando se pretende abordar el estudio de la física a nivel superior. En este sentido, y considerando que en los cursos iniciales de física se ajustan a la organización de los textos de física para ciencias e ingeniería, exigen tener una buena comprensión del objeto matemático función afín y parábola, para disminuir los obstáculos epistemológicos en la comprensión de la física.

Se ha identificado así que la noción de variable se estudia en la educación matemática apoyado en algunas ocasiones en contextos físicos, pero no hay una interrelación presente entre el estudio de ésta y la de los conceptos físicos, lo que hace que en la práctica se note la parcelación sin ni siquiera considerar la relación de dependencia que se ha planteado. En tal sentido, investigaciones como la planteada tienen un valor especial para lo que podría denominarse “la intersección” entre el campo de la matemática y la física.

Agradecimientos

La Fundación Universidad Autónoma de Colombia que, a través del Sistema Universitario de Investigaciones, financian el proyecto de investigación del que se deriva esta publicación. Al Departamento de Ciencias Naturales y Exactas, que apoya el desarrollo de la actividad docente investigativa, así como al Doctorado en Física Educativa del Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada CICATA, Unidad Legaría del Instituto Politécnico Nacional, México que, en cabeza del Dr. César Eduardo Mora Ley, colabora con la gestación de investigaciones en el campo de la física (http://www.cicata.ipn.mx/Paginas/Inicio.aspx).

Especial dedicatoria de este artículo a mis profesores, hoy compañeros de trabajo y guías de formación, Alejandro Hurtado Márquez y Luis Augusto Méndez, quienes han dedicado su vida a formar profesionales en la docencia de la física más allá del espacio de la clase.

¹ Artículo de revisión, resultado del proyecto de investigación “Nivel de comprensión del concepto de variable, meta cognición, estilo de aprendizaje y logro académico en una secuencia didáctica de la cinemática unidimensional. Financiado Fundación Universidad Autónoma de Colombia, a través del Sistema Universitario de Investigación SUI convocatoria 023. Cicata – IPN. , del Grupo de Investigación Ciencias Básicas, Matemáticas y su didáctica.
² Profesor Investigador de Física, Jefe de Área de Física y Química, Departamento de Ciencias Naturales y Exactas.  Fundación Universidad Autónoma de Colombia; Centro de Investigación de Ciencia Aplicada y Tecnología Avanzada del Instituto Politécnico Nacional CICATA-IPN posgrado en Física Educativa. oscar.suarez@fuac.edu.co

Referencias

Alzugaray, Gloria, Enrique, Claudio, & Esterkin, Carlos. (2014). Conceptos y preconceptos de cinemática y dinámica en ingresantes a carreras de ingeniería. En: Latin American Journal Physics Education Lajpe, Vol. 8 No 1(31-37).

André, C.F. (2009). A prática da pesquisa e mapeamento informacional bibliográfico apoiados por recursos tecnológicos: impactos na formação de professores. (Doctoral), Universidade De São Paulo. Recuperado de http://www.Teses.Usp.Br/Teses/Disponiveis/48/48134/Tde-15122009-095048/Pt-Br.Php

Apostol, Tom. (1999). Calculus Volumen 1-Cálculo con funciones de una variable, con una introducción al álgebra lineal. Barcelona-España: Editorial Revertré S.S. .

Bastién, G, Mora Ley, César Eduardo, & Sánchez, G. (2010). Obstáculos en la resolución de problemas en alumnos de bajo rendimiento. En: Latin American Journal Physics Education Lajpe, Vol. 4 No 3, 667-682.

Bravo Carrasco, Juan. (2005). Taylor revisitado la productividad es la clave es la hora de hacerle caso, las empresas y los paises ricos ya lo hicieron. Santiago De Chile: Editorial Evolución S.A.

Callaos, N. (2010). The Essence Of Engineering And Meta-Engineering: A Work In Progress. Documento presentado en Cuarta Conferencia Ibero-Americana de Ingeniería e Innovación Tecnológica: CIIIT 2012, Orlando, Florida Estados Unidos de América.

Cantoral, Ricardo, & Farfán, Rosa María. (2013). Pensamiento Y Lenguaje Variacional En La Introducción Al Análisis. Recuperado el 12 de Agosto de 2014 de http://Www.Fing.Edu.Uy/Imerl/Didactica_Matematica/Documentos_2008/Cantoral y Farfán (1998)-Epsilon.Pdf

Castiblanco, Ana, Urquina, Henry, & Acosta, Ernesto. (2004). Incorporación de las nuevas tecnologías al currículo de matemàticas de la educación matemática de la Educación Básica Secundaria y Media de Colombia. Bogotá D.C. Colombia Ministerio De Educación Nacional.

Cole, Michael. (1999). Psicología Cultural. Una disciplina del pasado en el presente. Madrid, España: Ediciones Morata.

Corona, Adrian, Sánchez, Maribel, Emma, González, & Slisko, Josip. (2012). Habilidades cognitivas y la resolución de un problema de cinemática: un estudio comparativo entre los estudiantes de secundaria, bachillerato y universidad. En: Latin American Journal Physics Education Lajpe, Vol. 6 No. 2, 292-299.

Fourez, Gérard. (2005). Alfabetización científica tecnológica: acerca de las finalidades de la enseñanza de las ciencias. Buenos Aires: Coliue.

Gil, Daniel, Macedo, Beatriz, Martinez, Joaquin, Sifredo, Carlos, Valdes, Pablo, & Vilches, Amparo. (2005). ¿Cómo promover el interés por la cultura científica? Una propuesta didáctica fundamentada para la educación científica de jóvenes de 15 a 18 años. Santiago De Chile: Andros Impresores-Unesco.

Gómez, Enrique (2007). La construcción de la noción de variable. Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada-Unidad Legaria, Instituto Politécnico Nacional, México DF-México.

Gómez, Víctor. (2006). La Cultura para el trabajo en la Educación Media en Bogotá. Bogotá D.C. Colombia: Publicaciones Instituto de Investigación en Educación.

Krieger, Martin. (1997, 1998). El maletín de herramientas del físico. En A. Tiberghien, L. Jossem & J. Barojas (Eds.), Libro De " I.C.P.E. " © International Commission On Physics Education 1997, 1998 "Resultados De investigaciones en didáctica de la física en la formación de docentes". Universidad Nacional Abierta U.N.A.-Venezuela: Publicado por la Comisión Internacional de la Enseñanza de la Física (ICPE).

Maury Mancilla, Erwin, Palmezano Sarmiento, Gregorio, & Cármaro Barrios, Sandro. (2012). Sistema de tareas para el desarrollo del pensamiento variacional en 5° grado de Educación Básica Primaria. En: Escenarios, Vol. 10 No. 1, 7-16.

Mcdermott, Lilian; Shaffer, Peter, &Physics Education Group at the University Of Washington. (2002). En: Tutorials in Introductory Physics. Upper Saddle River, NJ: Prentice-Hall.

Miranda, Isaías, Radford, Luis, & Guzman, José. (2013). Un origen matemático vs dos orígenes fenomenológicos: la significación del movimiento de objetos respecto del punto (0,0). En: REDIMAT Revista de investigación en didáctica de las matemáticas, Vol. 2 No. 2, 183-208.

Morales, Astrid, Mena, Jaime, Vera, Francisco, & Rivera, Rodrigo. (2012). El rol del tiempo en un proceso de modelación utilizando vídeos de experimentos físicos. En: Enseñanza de las ciencias, Vol 30 No 3, 237 -256.

Pareja Heredia, Diego. (2014). Taylorismo y educación matemática. Recuperado el 31 de agosto de 2014de http://Www.Matematicasyfilosofiaenelaula.Info/Articulos.Htm

Quintana, A. (2006). Metodología de investigación científica cualitativa. En A. Quintana & W. Montgomery (Eds.), Psicología: Tópicos de actualidad (Pp. 47-85). Lima, Perú: Escuela Académico Profesional-Facultad de Psicología

Redish, Edward, Steinberg, Richard, & Saul, Jeffery. (1996). Student Difficulties with Math in Physics: Giving Meaning to Symbols. Documento presentado en el College Park Meeting de AAPT.

Resnick, Robert, Halliday, David, & Krane, Kenneth. (1996). Física (Vol. 1). México DF, México: CECSA.

Rodríguez, A. Méndez, & Moya, M. Astudillo. (2008). La investigación en la era de la información (Trillas Ed. 1a Edición Ed.). México: Trillas.

Sears, Zemansky, Young, Hugh, & Freedman, Roger. (2009). Física Universitaria (Vol. 1). México DF, México: Pearson Educatión.

Serway, Raymond, & Jewett, John. (2008). Física para ciencias e ingeniería (Vol. 1). México DF, México: CENGAGE Learning.

Soledad Bos, Alejandra, Ganimian, Alejandro, & Vegas, Emiliana. (2014a). América Latina en PISA 2012-Brief #4: ¿Cuántos estudiantes logran desempeño destacado? En: B.-. Educación (Ed.), América Latina en PISA 2012 (Vol. No 14): Inter-American Development Bank.

_____________. (2014b). América Latina en PISA 2012-Brief #14: México en PISA 2012 Logros y desafios pendientes. En B.-. Educación (Ed.), América Latina en PISA 2012 (Vol. No 14): Inter-American Development Bank.

Soledad Bos, Alejandra, Ganimian, Alejandro, Vegas, Emiliana, & Horacio Álvarez, Marinelli. (2014). América Latina en PISA 2012-Brief #12: Colombia en PISA 2012 Logros y desafios pendientes. En B.-. Educación (Ed.), América Latina en PISA 2012 (Vol. No 14): Inter-American Development Bank.

Steinberg, Richard. (1997). Identifying and Addressing Student Difficulties with Mathematics when Learning Physics. Documento presentado en APS/AAPT, Washington, DC-Estados Unidos De América.

Steinberg, Richard, Oberem, Graham, & Mcdermott, Lilian. (1996). Development of a computer-based tutorial on the photoelectric effect. En: American Journal Of Physics, Vol 64

Steinberg, Richard, Saul, Jeffery, Wittmann, Michael, & Redish, Edward. (1996). Student difficulties with math in physics: why can't students apply what they learn in math class? Documento presentado en AAPT Meeting, College Park, University of Maryland.

Steinberg, Richard, Wittmann, Michael, & Redish, Edward. (1996). Mathematical Tutorials in Introductory Physics. Documento presentado en The International Conference On Undergraduate Physics Education (ICUPE), College Park, Maryland. Http://Www.Physics.Umd.Edu/Perg/Papers/Redish/Icupemsc.Htm

Stewart, James, Redlin, Lothar, & Watson, Saleem. (2012). Precálculo matemáticas para el cálculo-Sexta Edición. México: Cengage Learning Editores.

Suárez, Óscar, & Hurtado, Alejandro. (2012a). El experimento en la formación de ingenieros: aproximación epistemológica. En: Revista Educyt Asociación colombiana para la investigación en educación en ciencias y tecnología, volumen extraordinario, diciembre,, 29-43

_________. (2012b). Laboratorios didácticos de física orientados a la formación de ingenieros: un trabajo en desarrollo. En: Revista argentina de enseñanza de la ingeniería, Año 13 No 23 7-25.

___________. (2013). Implementación de una estrategia para el desarrollo de competencias básicas desde los laboratorios didácticos de física que se desarrollan en la Universidad Autónoma de Colombia: Fundación Universidad Autónoma De Colombia.

Tejeda, Santa. (2009). Diseño de una actividad educativa tipo tutorial para la comprensión de gráficas de cinemática. (Magíster). Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada Instituto Politécnico Nacional, México DF, México

Tejeda, Santa & Alarcón, Hugo. (2012). A Tutorial-Type Activity to Overcome Learning Difficulties in Understanding Graphics in Kinematics. En: Latin American Journal Physics Education Lajpe, Vol 6 No Suplementario, 285-289.

Trigueros, María, Reyes, A, Ursini, Sonia, & Quintero, R. (1996). Diseño de un cuestionario de diagnóstico acerca del manejo del concepto de variable en el álgebra. En: Enseñanza de las ciencias, Vol 14 No 3, 351-363.

Ursini, Sonia, & Trigueros, Maria (2006). ¿Mejora la comprensión del concepto de variable cuando los estudiantes cursan matemáticas avanzadas? En: Educación Matemática, Vol. 18 No 3, 5-38.

Vasco, Carlos. (2009-2010). El pensamiento variacional y la modelación matemática. En: Http://Pibid.Mat.Ufrgs.Br/2009-2010/Arquivos_Publicacoes1/Indicacoes_01/Pensamento_Variacional_VASCO.Pdf

Vega, Escalante, Juana Elisa, & Borges Cuesta, Abraham. (2012). Dificultades para comprender el concepto de variable: un estudio con estudiantes universitarios. Educación Matemática- Grupo Santillana México, Vol. 24 No 1, 107-132.

Villa Ochoa, Jhony Alexander. (2011). La comprensión de la tasa de variación para una aproximación al concepto de derivada. Un análisis desde la teoría de Pirie y Kieren. (Doctor), Universidad de Antioquia, Medellín Colombia.

Villa Ochoa, Jhony Alexander, & Ruiz Vahos, Mauricio (2010). Pensamiento variacional: seres-humanos-con-geogebra en la visualización de noción variacional. Investigación en educación matemática Sao Paulon Brasil, Vol. 12 No 3, 514-528.

Wagner, Sigrid. (1983). What Are These Things Called Variables? En: Mathematics Teacher, Vol 76, 474-479.

Wartofsky, Max. (1973). Filosofía de la ciencia (Vol. 1). Edición en Español. Madrid-España: Alianza Editorial

___________. (1979). Models: Representation and the scientific understanding (Vol. XLVIII). London, England: D. Reidel Publishing Understanding.